Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.1 - Ex. 18
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.
18.Se existir , então também existem e .
Passo 1
Quando o limite de uma função em um determinado ponto existe, é porque, necessariamente, os limites laterais desse ponto existem: eles são a causa da existência do limite “não lateral”.
Tomemos como exemplo uma função muito simples, como a :
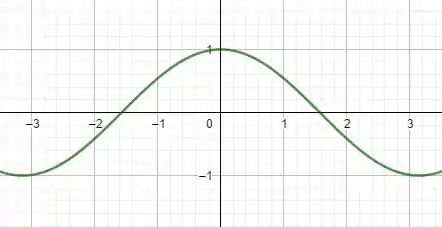
Se calculamos , pelo gráfico já vemos facilmente que isso resulta em . Isso porque os limites laterais e existem, são iguais, e ambos valem também .
Assim, isso é que causa a existência do limite no ponto escolhido Portanto, a afirmação é verdadeira!
Resposta
Verdadeira.
Exercícios de Livros Relacionados
Seja f ( x ) a função definida pelo gráfico:Intuitivamente, encontre se existir:a) lim x → 1 + f ( x )
Definir uma função y = g ( x ) tal que lim x → 2 g x = 4 , mas g x não é definida em x = 2 .
Mostrar que lim x → 3 x 2 = 9 .
Descrever analítica e graficamente uma função y = f ( x ) tal que lim x → 3 f x não existe e lim x → 6 f x existe.
Seja f ( x ) a função definida pelo gráfico:Intuitivamente, encontre se existir:d) lim x → + ∞ f ( x )