Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 3.6 - Ex. 7
Definir uma função tal que , mas não é definida em .
Passo 1
Então galera, antes começar a resolução vale ressaltar que existem INFINITOS exemplos de funções que atendem as características dadas pelo enunciado, tudo bem? O que vamos fazer aqui é utilizar apenas uma, que já será o suficiente! A primeira característica que a função tem que ter é ter os limites laterais quando iguais, ou seja, quando pela direita tem que ser igual quando pela esquerda, então podemos pegar uma função qualquer que resulte em quando se aproxima de , saca só:
Essa é a primeira característica, ok? Então vamos para a próxima!
Passo 2
A segunda característica que a função tem que ter é não ser definida em . Para fazermos isso também não é muito difícil, basta pegarmos uma função que resulte em também, assim como a que escolhemos no passo anterior, mas que só é definida para , como essa aqui ó:
Essa descrição foi a parte analítica da coisa, tudo bem galera? Para facilitar a visualização, podemos escrever as funções assim ó:
Por fim, fazendo a descrição gráfica, ou seja, plotando o gráfico dessas funções, teremos:
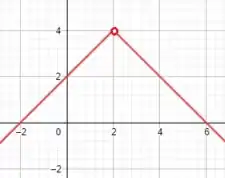
E está aí nossas descrições! 😊
Resposta
