Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.6 - Ex. 17

Determine a área exata da superfície z = 1 + 2 x + 3 y + 4 y 2 , 1 ≤ x ≤ 4 , 0 ≤ y ≤ 1 .

Passo 1

Faala, beleza?

Essa questão pede pra gente calcular a área exata de uma superfície...

Vamos usar essa fórmula aqui:

A S = ∬ D 1 + f x 2 + f y 2 d A

Onde S é a superfície determinada pelo gráfico de z = f x , y no domínio D .

Então vamos ver quem é f , pra calcular as derivadas parciais.

Depois, vamos definir o domínio D , pra transformar essa integral em integral iterada, e usar um software pra calcular (vou usar o WolframAlpha)!

Passo 2

A equação da área que o problema deu define quem é a função f :

f x , y = z = 1 + 2 x + 3 y + 4 y 2

Calculamos as derivadas parciais.

De x , com y constante:

f x = ∂ 1 + 2 x + 3 y + 4 y 2 ∂ x = 2

E em função de y , com x constante:

f y = ∂ 1 + 2 x + 3 y + 4 y 2 ∂ y = 3 + 8 y

Substituindo na integral:

A S = ∬ D 1 + f x 2 + f y 2 d A

= ∬ D 1 + 2 2 + 3 + 8 y 2 d A

Então a integral que queremos calcular é:

A S = ∬ D 5 + 3 + 8 y 2 d A

Passo 3

Agora vamos olhar pro domínio pra transformar em integral iterada:

1 ≤ x ≤ 4

0 ≤ y ≤ 1

Como já temos os limites das variáveis, a integral fica:

A S = ∫ 0 1 ∫ 1 4 5 + 3 + 8 y 2 d x d y

Agora vamos usar o WolframAlpha pra determinar o valor exato dessa integral:

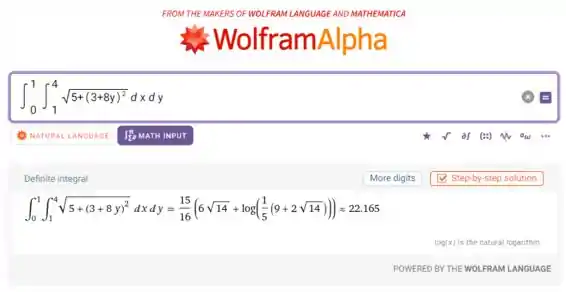
Nossa resposta, então, fica:

A S = 15 16 6 14 + ln ⁡ 1 5 9 + 2 14

Que é a mesma coisa que:

A S = 45 8 14 + 15 16 ln ⁡ 9 + 2 14 5

Resposta

A S = 45 8 14 + 15 16 ln ⁡ 9 + 2 14 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Xavier e Yolanda têm aulas que terminam ao meio-dia e concordaram em se encontrar todo dia depois das aulas. Eles chegam em um café separadamente. O tempo de chegada de Xavier é X e o da Yolanda é Y ,
(a) Uma luminária tem duas lâmpadas de um tipo com tempo de vida médio de 1000 horas. Supondo que possamos modelar a probabilidade de falha dessas lâmpadas por uma função densidade exponencial com méd
Quando estudamos uma contaminação epidêmica, supomos que a probabilidade de um indivíduo infectado disseminar a doença para um indivíduo não infectado seja uma função da distância entre eles. Consider
Suponha que X e Y sejam variáveis aleatórias, onde X tem distribuição normal com média 45 e desvio-padrão 0,5 e Y tem distribuição normal com média 20 e desvio-padrão 0,1 .(a) Encontre P 40 ≤ X ≤ 50,
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D = x , y | 0 ≤ x ≤ a ,0 ≤ y ≤ b ; ρ x , y = 1 + x 2 + y 2