Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.5 - Ex. 33

Quando estudamos uma contaminação epidêmica, supomos que a probabilidade de um indivíduo infectado disseminar a doença para um indivíduo não infectado seja uma função da distância entre eles. Considere uma cidade circular com raio de 10   k m na qual a população está uniformemente distribuída. Para um indivíduo não infectado no ponto A x 0 ,   y 0 , suponha que a função probabilidade seja dada por

f P = 1 20 20 - d P ,   A

onde d P ,   A denota a distância de P a A .

(a) Suponha que a exposição de uma pessoa à doença seja a soma das probabilidades de adquirir a doença de todos os membros da população. Suponha ainda que as pessoas infectadas estejam uniformemente distribuídas pela cidade, existindo k indivíduos contaminados por quilômetro quadrado. Determine a integral dupla que representa a exposição de uma pessoa que reside em A .

(b) Calcule a integral para o caso em que A está no centro da cidade e para o caso em que A está na periferia da cidade. Onde seria preferível viver?

Passo 1

Vamos lá galera, tudo certo? Temos uma função que representa a probabilidade de um individuo se contaminar com uma doença em relação à distância a um ponto A.

f P = 1 20 20 - d P ,   A

Precisamos enonctrar uma forma de escrever matematicamente a integral que representa a exposição de uma pessoa que vive em A, de uma maneira geral, e também para os casos em que A reside no interio e na preferia da cidade. Veja que precisaremos nos recordar como escrever a distância absoluta entre dois pontos para substituir na função. Tudo certo por aqui? Então vamos.

Passo 2

  1. Pessoal, como há k indivíduos contaminados por quilômetro quadrado, podemos escrever a integral dupla que representa a exposição assim:

    2. E = ∫ ∫ D   k   f P ,   A   d A = k ∫ ∫ D   20 - d P ,   A 20   d A

    Veja que: k ∫ ∫ D   20 - d P ,   A 20   d A =   k ∫ ∫ D   20 20 - d P ,   A 20   d A

    Lembrando que podemos utilizar o o teorema de pítágoras para encontrar a distância entre dois pontos.

    = k ∫ ∫ D   1 - x - x 0 2 + y - y 0 2 20   d x   d y

    Passo 2

  2. Se A está no centro da cidade, então x 0 ,   y 0 = 0 ,   0 . A integral ficará assim:

E = k ∫ ∫ D   1 - x 2 + y 2 20   d x   d y = k ∫ 0 2 π ∫ 0 10 1 - r 20   r   d r   d θ = 2 π k r 2 2 - r 3 60 0 10

= 2 π k 50 - 50 3 = 200 π 3 k ≈ 209   k

Passo 3

O exercício nos pode também que seja calculado a integral dupla se A estiver na periferia.

Para A na periferia, é mais conveniente usar um sistema de coordenadas polares centrado em A , como mostra a seguinte figura:

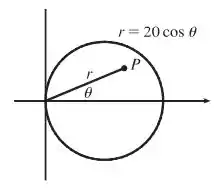
Então a integral vai ficar assim:

E = k ∫ - π 2 π 2 ∫ 0 20 cos ⁡ θ 1 - r 20   r   d r   d θ = k ∫ - π 2 π 2 r 2 2 - r 3 60 0 20 cos ⁡ θ d θ

Aplicando os limites de integração e simplificando.

= k ∫ - π 2 π 2 200 cos 2 ⁡ θ - 400 3 cos 3 ⁡ θ d θ = 200   k ∫ - π 2 π 2 1 2 + 1 2 cos ⁡ 2 θ - 2 3 1 - s e n 2   θ cos ⁡ θ d θ

Resolvendo a integral:

= 200   k 1 2 θ + 1 4 s e n   2 θ - 2 3 s e n   θ + 2 3   . 1 3 s e n 3   θ - π 2 π 2

Aplicando os limites de integração e fazendos a álgebra.

= 200   k π 4 + 0 - 2 3 + 2 9 + π 4 + 0 - 2 3 + 2 9 = 200 π 2 - 8 9 k ≈ 136   k

Como a exposição na periferia é bem menor do que no centro ( 136   k < 209   k ) , é preferível viver na periferia.

Resposta

(a) k ∫ ∫ D   1 - x - x 0 2 + y - y 0 2 20   d x   d y

(b) Centro: 200 π 3 k ≈ 209   k

Periferia: 200 π 2 - 8 9 k ≈ 136   k

É preferível viver na periferia.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que X e Y sejam variáveis aleatórias, onde X tem distribuição normal com média 45 e desvio-padrão 0,5 e Y tem distribuição normal com média 20 e desvio-padrão 0,1 .(a) Encontre P 40 ≤ X ≤ 50,
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D = x , y | 0 ≤ x ≤ a ,0 ≤ y ≤ b ; ρ x , y = 1 + x 2 + y 2
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D = x , y | 1 ≤ x ≤ 3 ,1 ≤ y ≤ 4 ; ρ x , y = k y 2
Determine a massa e o centro de massa da l��mina que ocupa a região D e tem função densidade ρ .D é limitada por y = 1 - x 2 e y = 0 ; ρ x , y = k y .