(a) Uma luminária tem duas lâmpadas de um tipo com tempo de vida médio de horas. Supondo que possamos modelar a probabilidade de falha dessas lâmpadas por uma função densidade exponencial com média , determine a probabilidade de que ambas as lâmpadas venham a falhar dentro de um período de horas.

(b) Outra luminária tem somente uma lâmpada do mesmo tipo das da parte (a). Se a lâmpada queima e é trocada por outra do mesmo tipo, determine a probabilidade de que as duas venham a falhar dentro de horas.

1. Galera, o exercício nos disse que dá pra modelar a probabilidade de falha de cada lâmpada por uma função densidade exponencial.

Como a média é , podemos escrever:

E agora é só multiplicarmos as duas:

E essa é nossa equação procurada em função de e .

Então, pra calcular a probabilidade de ambas falharem dentro de horas, fazemos assim:

Substituindo a função que encontramos no passo anterior, já separando em um produto de duas integrais, cada qual com seu respectivo limite de integração:

Resolvendo cada integral:

Finalmente, aplicando os limites de integração:

Temos:

(b) Nesse caso, para que as duas falhem dentro de horas, teremos que a soma dos tempos de falha de cada uma seja no máximo :

Ou seja, é:

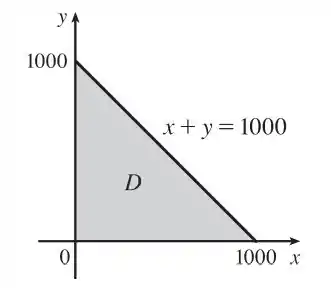
a região onde

Dessa forma, podemos reescrever como:

Então já temos os limites de integração da nossa integral dupla:

Integrando por dentro em , tratando como constante:

Aplicando os intervalos de integração:

Agora finalmente integramos em :

Aplicando os intervalos:

Somando os termos: