Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.4 - Ex. 32

Xavier e Yolanda têm aulas que terminam ao meio-dia e concordaram em se encontrar todo dia depois das aulas. Eles chegam em um café separadamente. O tempo de chegada de Xavier é X e o da Yolanda é Y , onde X e Y são medidos em minutos após o meio-dia. As funções densidade individuais são

f 1 x = e - x ,     s e   x ≥ 0 0 ,     s e   x < 0 f 2 y = 1 50 y ,     s e   0 ≤ y ≤ 10 0 ,     c a s o   c o n t r á r i o

(Xavier chega algumas vezes depois do meio-dia, e é mais provável que ele chegue na hora do que se atrase. Yolanda sempre chega às 12 h 10 e é mais provável que se atrase do que chegue pontualmente.) Depois de Yolanda chegar, ela espera até meia hora por Xavier, mas ele não espera por ela. Determine a probabilidade de eles se encontrarem.

Passo 1

Tudo belezinha, galera?

Então, a questão é enorme, mas vamos ver o que ela quer nos dizer, show?

Xavier e Yolanda vão se encontrar ao meio-dia. Xavier chega no tempo X definido pela função densidade:

f 1 x = e - x ,     s e   x ≥ 0 0 ,     s e   x < 0

E Yolanda chega no café no tempo Y definido pela função densidade:

f 2 y = 1 50 y ,     s e   0 ≤ y ≤ 10 0 ,     c a s o   c o n t r á r i o

Com isso, temos algumas informações:

(1º) Xavier chega algumas vezes depois do meio-dia, e é mais provável que ele chegue na hora do que se atrase;

(2º) Yolanda sempre chega às 12 h 10 e é mais provável que se atrase do que chegue pontualmente.

Nesse dia que marcaram de se encontrar, depois de Yolanda chegar, ela espera até meia hora por Xavier, mas ele não espera por ela.

Precisamos saber a probabilidade de eles se encontrarem.

Galera, primeiro vamos escrever como fica a função densidade conjunta:

f x ,   y = f 1 x ⋅   f 2 y

Ou seja,

1 50 e - x y ,     s e   x ≥ 0 ,   0 ≤ y ≤ 10 0 ,     c a s o   c o n t r á r i o

Passo 2

Show! Agora repare que, para os dois se encontrarem, Yolanda deve chegar antes de Xavier, então, X ≥ Y . E como ela só espera por meia hora, também devemos ter X - Y ≤ 30 . Fazendo um esboço dessa região, fica assim:

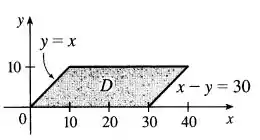
Ou seja, a integral que calcula a probabilidade dos dois se encontrarem vai ser definida pelos seguintes limites de integração:

0 ≤ y ≤ 10

E para o eixo x :

x - y = 30 → x = 30 + y

Por isso,

y ≤ x ≤ 30 + y

Assim:

∫ 0 10 ∫ y y + 30 1 50 e - x y   d x   d y

Passo 3

Agora vamos calcular a integral, começando de dentro da fora, ou seja, primeiro em relação a x :

∫ 0 10 ∫ y y + 30 1 50 e - x y   d x   d y

∫ 0 10 1 50 y - e - x y y + 30 d y

Substituindo pelos limites de integração:

∫ 0 10 1 50 y - e - 30 e - y + e - y   d y

Organizando, chegaremos a

∫ 0 10 1 - e - 30 50   y e - y d y

Integrando agora em relação a y :

1 - e - 30 50 - y e - y - e - y 0 10

Substituindo pelos limites:

1 - e - 30 50 - 10 e - 10 - e - 10 + 0 + 1

1 - e - 30 1 - 11 e - 10 50 ≈ 0,020

Resposta

0,020

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é uma região triangular com vértices 0 ,0 ,2 ,1 ,0 ,3 ; ρ x ,y = x + y
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é a região triangular delimitada pelas retas x = 0,y = x e 2 x + y = 6 ; ρ x ,y = x 2
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é delimitada por y = e x,y = 0,x = 0 e x = 1 ; ρ x ,y = y
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é delimitada por y = x,y = 0 e x = 1 ; ρ x ,y = x
A função densidade conjunta para um par de variáveis aleatórias X e Y é f x ,y = C x ( 1 + y ) , s e0 ≤ x ≤ 1,0 ≤ y ≤ 2 0 , c a s oc o n t r á r i o á (a) Determine a constante C .(b) Determine P X ≤