Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.4 - Ex. 32

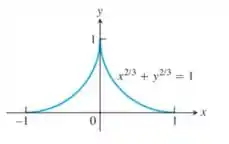
Determine a área da superfície gerada pela rotação do eixo x do pedaço de astroide

x 2 3 + y 2 3 = 1 mostrado na figura a seguir. (Sugestão: gire o pedaço do primeiro quadrante

y = 1 - x 2 3 3 2 ,   0 ≤ x ≤ 1 ,   em torno do eixo x e dobre o resultado.)

Passo 1

Por definição temos que se a função f x ≥ 0   é continuamente derivável em [ a , b ] , a área da superfície gerada pela rotação da curva y = f ( x ) em torno do eixo x é:

S = ∫ a b 2 π f x 1 + f ' x 2   d x

Assim, seguindo a sugestão temos que:

S = 2 ∫ 0 1 2 π   1 - x 2 3 3 2 1 + 3 2 ( 1 - x 2 3 ) 1 2 × 2 3 x - 1 3 ) 2       d x =

= 4 π ∫ 0 1 1 - x 2 3 3 2 1 + 1 - x 2 3   1 2 2 x 1 3 2     d x = 4 π ∫ 0 1 1 - x 2 3 3 2 ( x 2 3 + ( 1 - x 2 3 ) ) × 1 x 2 3     d x =

= 4 π ∫ 0 1 1 - x 2 3 3 2 × 1 x 1 3   d x

Passo 2

Para essa integral devemos aplicar a integração por substituição . Esse método consiste em fazer uma troca de uma parte de uma função f ( x ) por uma variável simples ( u ) e que resulte em um d u = f ’ ( x ) conveniente que irá possibilitar a integração, geralmente esse resultado é parte de outra função contida no integrando. Após integrar, você deve substituir a variável simples pela função que você a usou para substituir.

u = 1 - x 2 3                         d u = - 2 3 x - 1 3   d x ⇒ - 3 2 d u = x - 1 3   d x

Passo 3

Aplicando a substituição temos que:

= 4 π ∫ 0 1 1 - x 2 3 3 2 × 1 x 1 3   d x = - 4 π × 3 2 ∫ 0 1 u 3 2   d u = - 6 π ∫ 0 1 u 3 2   d u

Passo 4

Calculando a integral:

- 6 π ∫ 0 1 u 3 2 d u = - 6 π u 5 2 5 2 1 0 = - 12 π 5 u 5 2 1 0  

Lembre-se que a integração de um polinômio de forma genérica é dada por:

∫ x n d x = x n + 1 n + 1 + C

Passo 5

Por fim substituiremos u pela função que atribuímos e os limites de integração. Relembrando que de forma genérica ele é feito da seguinte maneira:

∫ a b f x d x = F b - F ( a )

Ou seja, após integrar de forma genérica você irá substituir os limites de integração ( a e b) nesse resultado obtido, respeitando a ordem de o limite superior aplicado na função menos o limite inferior aplicado na função.

Assim:

- 12 π 5 u 5 2 1 0 = - 12 π 5 1 - x 2 3 5 2   1 0 = - 12 π 5 1 - 1 2 3 5 2 - 1 - 0 5 2 = 12 π 5

Resposta

12 π 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área da superfície gerada pela rotação da curva em torno do eixo indicado. x = e y + e - y 2 ,0 ≤ y ≤ l n l n2; e i x oy
Determine a área da superfície gerada pela rotação da curva em torno do eixo indicado. x = y 4 4 + 1 8 y 2 , 1 ≤ y ≤ 2 ; e i x ox Sugestão: Expresse d s = d x 2 + d y 2 em termos de d y , e calcule a
Determine a área da superfície gerada pela rotação da curva em torno do eixo indicado. y = 1 3 x 2 + 2 3 2 , 0 ≤ y ≤ 2 ; e i x oy Sugestão: Expresse d s = d x 2 + d y 2 em termos de d x , e calcule a
Escreva uma integral para a área da superfície gerada pela rotação da curva y = c o s c o sx,- π 2 ≤ x ≤ π 2 , em torno do eixo x .
Demonstre que a área da superfície de uma esfera de raio a ainda é 4 π a 2 usando a Equação 3 para determinar a área da superfície gerada pela rotação da curva y = a 2 - x 2, - a ≤ x ≤a , em torno do