Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.6 - Ex. 13
Determine a área da superfície com precisão de quatro casas decimais, expressando a área em termos de integral de função de uma variável real e use sua calculadora para estimar o valor da integral.
A parte da superfície que está acima do círculo .
Passo 1
Faala, pessoal!
Nessa questão a gente vai ter que calcular a área de uma superfície, usando uma calculadora pra estimar com precisão de quatro casas decimais.
Pra isso, vamos usar que a área da superfície definida por em um domínio é dada por:
Então, a primeira coisa vai ser usarmos a função pra calcular as derivadas parciais.
Depois, vamos definir o domínio e transformar a integral em uma integral iterada.
Por último, vamos transformar essa integral dupla em uma integral simples, e usar um software pra estimar o valor dela – vou usar o WolframAlpha.
Passo 2
O enunciado fala qual a expressão da superfície:
Então vamos calcular as derivadas parciais.
Derivando em função de , consideramos constante. Vamos usar a regra da cadeia:
Como a derivada da exponencial é ela mesma:
Derivando em função de , mantemos constante e também vamos usar a regra da cadeia:
Então:
Substituindo na integral:
Abrindo o quadrado:
Podemos colocar e em evidência:
Passo 3
O nosso domínio é definido por
Isso é uma região circular:
Então vamos fazer uma mudança de variáveis para coordenadas polares:
Com e
Dessas coordenadas, temos,
Lembrando que o jacobiano, que vamos multiplicar dentro do integrando, é
Assim, a integral fica:
Passo 4
Agora vamos calcular essa integral, de dentro pra fora:
Primeiro integramos em função de , considerando constante.
Como o integrando todo depende só de , podemos tirar dessa primeira integral:
Então, a área da superfície se resume a uma integral simples assim:
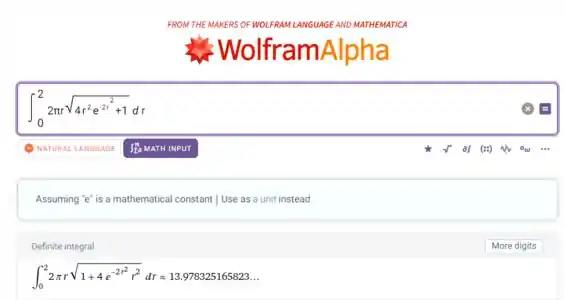
Ou seja,