Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.6 - Ex. 3

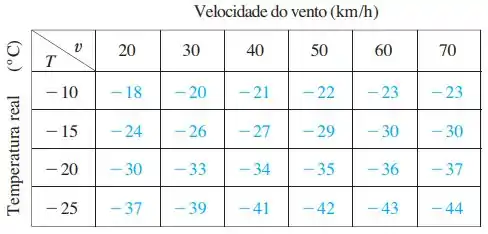
Uma tabela de valores do índice de sensação térmica W = f ( T , v ) é dada no Exercício 3 da Seção 14.3. Use-a para estimar o valor de D u f ( - 20,30 ) , onde u = ( i + j ) / 2 .

Passo 1

Para calcular D u f ( - 20,30 ) , vamos usar a equação

D u f x , y = f x x , y a + f y ( x , y ) b

Onde ( a , b ) é o vetor direção unitário, nesse caso f = f ( T , v ) e u = 1 2 , 1 2 , então

D u f T , v = f T T , v 1 2 + f v ( T , v ) 1 2

Para isso, vamos ter que estimar os valores de f T e f v usando a tabela.

f T ( T , v ) = lim h → 0 ⁡ f T + h , v - f ( T , v ) h

Como não temos a função para calcular o limite, vamos usar o menor h que conseguimos para aproximar a derivada, neste caso h = ± 5 , então primeiro com h = + 5

f T - 20 , 30 ≈ f - 20 + 5 , 30 - f ( - 20 , 30 ) 5

= f - 15 , 30 - f ( - 20,30 ) 5 = - 26 - ( - 33 ) 5

f T - 20,30 ≈ 7 5 = 1,4

Agora com h = - 5

f T - 20,30 ≈ f - 20 - 5,30 - f ( - 20,30 ) - 5

= f - 2 5,30 - f ( - 20,30 ) - 5 = - 39 - ( - 33 ) - 5

f T - 20,30 ≈ - 6 - 5 = 1 , 2

Tirando a média entre as duas

f T - 20,30 ≈ 1,4 + 1,2 2 = 1,3

Passo 2

De forma semelhante vamos estimar f v ( - 20,30 ) , mas o menor h que conseguimos é h = ± 10 , então primeiro com h = + 10

f v - 20,30 ≈ f - 20,30 + h - f ( - 20,30 ) h

= f - 20,30 + 10 - f ( - 20,30 ) 10 = f - 20 , 40 - f ( - 20,30 ) 10

= - 34 - ( - 33 ) 10 = - 1 10 = - 0,1

Agora com h = - 10

f v - 20,30 ≈ f - 20,30 + h - f ( - 20,30 ) h

= f - 20,30 - 10 - f ( - 20,30 ) - 10 = f - 20 , 2 0 - f ( - 20,30 ) - 10

= - 3 0 - ( - 33 ) - 10 = 3 - 10 = - 0 , 3

Tirando a média

f v - 20,30 ≈ - 0,1 - 0,3 2 = - 0,2

Passo 3

Substituindo na fórmula

D u f T , v = f T T , v 1 2 + f v ( T , v ) 1 2

D u f - 20 , 30 ≈ 1,3 1 2 + - 0,2 1 2 = 1,1 1 2

D u f - 20,30 ≈ 0,7778

Resposta

D u f - 20,30 ≈ 0,7778

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a derivada direcional de f ( x , y ) = x . y em P 2,8 na direção de Q 5,4 .