Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 4.3 - Ex. 1d

Calcule o centro de massa

Passo 1

Através da integral dupla, as coordenadas do centro de massa de um conjunto B são dadas por:

x_c = (int int_B x d m)/(int int_B d m)

y_c = (int int_B y d m)/(int int_B d m)

Onde o elemento de massa é dado por:

d m = delta (x , y) d x d y

Neste caso, B é dado por:

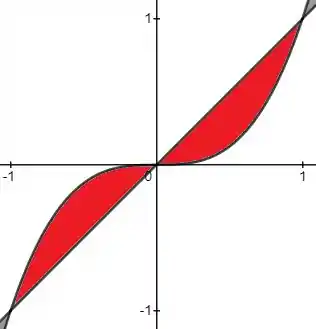
Só que só vamos pegar a região com 0 <= x <= 1 , pois é a única que se encaixa na restrição de B, onde:

x^3 <= y <= x

Além de que:

delta (x , y) = 1

Passo 2

A massa de B é dada por:

int int_B d m = int_0^1 [int_(x^3)^x (1) d y] d x

= int_0^1 [y] | [[x],[x^3]] d x

Substituindo o intervalo de integração:

= int_0^1 [x - x^3] d x

= [(x^2)/(2) - (x^4)/(4)] | [[1],[0]]

Assim:

= [(1)/(2) - (1)/(4)] = (1)/(4)

Passo 3

Assim, para a coordenada x do centro de massa teremos:

int int_B x d m = int_0^1 [int_(x^3)^x (x) d y] d x

= int_0^1 x [y] | [[x],[x^3]] d x

Substituindo o intervalo de integração:

= int_0^1 x [x - x^3] d x

= int_0^1 [x^2 - x^4] d x

= [(x^3)/(3) - (x^5)/(5)] | [[1],[0]]

Assim:

= [(1)/(3) - (1)/(5)] = (2)/(15)

Passo 4

Já para a coordenada y do centro de massa teremos:

int int_B y d m = int_0^1 [int_(x^3)^x (y) d y] d x

= int_0^1 [(y^2)/(2)] | [[x],[x^3]] d x

Substituindo o intervalo de integração:

= (1)/(2) int_0^1 [x^2 - x^6] d x

= (1)/(2) [(x^3)/(3) - (x^7)/(7)] | [[1],[0]]

Assim:

= (1)/(2) [(1)/(3) - (1)/(7)] = (2)/(21)

Passo 5

Logo, substituindo esses resultados nas equações, o centro de massa estará localizado em:

x_c = ((2)/(15))/((1)/(4)) = (8)/(15)

E

y_c = ((2)/(21))/((1)/(4)) = (8)/(21)

Logo:

((8)/(15) , (8)/(21))

Resposta

((8)/(15) , (8)/(21))

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área da superfície.A parte da esfera x 2+ y 2+ z 2= a 2 que está dentro do cilindro x 2 + y 2 = a x e acima do plano x y .
Determine a área exata da superfície z = 1 + 2 x + 3 y + 4 y 2 , 1 ≤ x ≤ 4 , 0 ≤ y ≤ 1 .
Determine a área da superfície.A Parte do paraboloide hiperbólico z = y 2 - x 2 que está entre os cilindros x 2 + y 2 = 1 e x 2 + y 2 = 4
Determine a área da parte finita do paraboloide y = x 2 + z 2 limitado pelo plano y = 25 .
A figura mostra a superfície criada quando o cilindro y 2 + z 2 = 1 intercepta o cilindro x 2 + z 2 = 1 . Determine área dessa superfície