Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.6 - Ex. 43
Determine a área de superfície.
A parte da esfera que está dentro do cilindro
Passo 1
Olá, tudo bem? Vamos ver o que a questão quer!
Ela diz para encontrar a área da superfície da esfera
Que está dentro do cilindro
Basicamente teremos parte de uma esfera dentro que um cilindro, e queremos achar a área dessa esfera que está dentro do cilindro. Algo semelhante a isso:
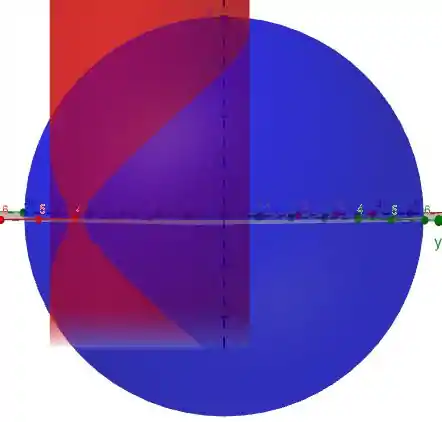
Como temos uma esfera, vamos usar coordenadas esféricas:
Sendo o raio da esfera.
Lembrando que para calcular a área de superfície de uma esfera, temos a seguinte fórmula:
Sendo o módulo do rotacional das derivadas parciais da esfera parametrizada.
O caminho que vamos seguir é:
Calcularemos as derivadas parciais para acharmos o módulo do rotacional, depois acharemos os limites de integração e finalmente, montaremos e resolveremos a integral.
Bora lá?
Passo 2
Primeiro, como temos duas áreas, uma acima de e outra abaixo e elas são idênticas, pois é a mesma esfera no mesmo cilindro. Vamos igualar essa área total na soma das duas áreas.
Seja a área da superfície da porção da superfície que se encontra acima do plano .
Então
Agora vamos parametrizar essa superfície :
Representando parametricamente, usando coordenadas esféricas:
Essas são as coordenadas da esfera, parametrizando:
Calculando a derivada parciais de em relação à :
Calculando a derivada parciais de em relação à :
Aplicando o produto vetorial :
Calculando esse determinante e depois tirando o módulo do vetor, temos
Passo 3
Agora vamos achar os limites de integração.
Como dividimos a área da esfera em duas, delimitada pelo plano
Temos que varia de até , pois ele só vai até a metade. Assim
Agora vamos achar os limites de :
Temos que a esfera tem que estar dentro do cilindro:
Substituindo coordenadas esféricas:
Dividindo tudo por
Podemos colocar em evidencia:
Usando a propriedade trigonométrica
Dividindo por :
Quando for positivo, também tem que ser.
Para positivo:
Então, para ser positivo:
Mas não acaba por aí!
Utilizando outra propriedade trigonométrica :
Aplicando :
Reorganizando:
Repare que esse valor é máximo quando e mínimo quando , porém varia entre a . Então, precisamos ajustar isso:
Agora, quando ,
Consequentemente
E sendo
Passo 4
Então, agora podemos calcular a integral dupla de :
Substituindo tudo que achamos:
Lembrando que o limite com mais variáveis fica no interior.
Resolvendo para :
Resolvendo para :
Aplicando os limites de integração:
Assim,
Como,
Temos que a área total é