Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.5 - Ex. 10
Determine a massa e o centro de massa da lâmina que ocupa a região e tem função densidade .
10. é limitada pelas parábolas e ;
Passo 1
Galera, tudo belê?
A questão quer a massa e o centro de massa da lâmina numa região , que no nosso caso, é limitada por essas parábolas aqui, ó:
E tem como função densidade .
Tanto para a massa quanto para o centro de massa existem fórmulas que iremos substituir, mas primeiro precisamos descobrir os limites de integração dessa nossa região .
Esboçando nosso gráfico, temos no primeiro octante
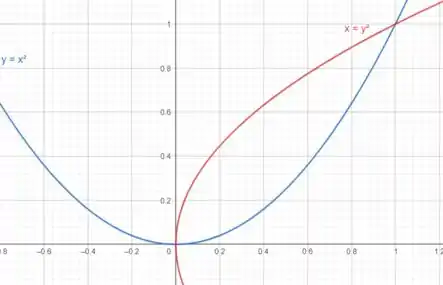
Observa que, se escolhermos a integral como do tipo I, o nosso eixo terá pontos definidos, que no gráfico a região de intersecção é enquanto no eixo temos de até:
Passo 2
Primeiro vamos calcular a massa. A fórmula é essa:
Substituindo tudo o que sabemos, ficaremos com:
Resolvendo logo a integral de dentro, ou seja, primeiro em relação a :
Substituindo pelos limites de integração, ficaremos com um novo integrando, e fazemos agora em relação a :
Show? 😉
Passo 3
Agora vamos calcular o centro de massa .
Primeiro
onde é o momento em relação ao eixo , calculado da seguinte forma:
Como temos cada um dos termos...
Resolvendo de dentro para fora:
Então,
Passo 4
Show! Agora só falta calcular , mas primeiro, vamos calcular o momento em relação ao eixo :
Integrando em relação a primeiro:
Substituindo, chegamos a
Portanto,
Então, o centro de massa é