Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.6 - Ex. 45

Determine a área de superfície.

A superfície com equações paramétricas x = u v . y = u + v , z = u - v , u 2 + v 2 ≤ 1

Passo 1

Iai gente, beleza?

O exercício quer que a gente ache a área da superfície com equações paramétricas:

x = u v

y = u + v

z = u - v

onde , u 2 + v 2 ≤ 1 .

Isso quer dizer que r ( u , v ) = ( u v , u + v , u - v )

Para determinar a área de uma superfície A parametrizada r ( u , v ) precisamos utilizar a seguinte fórmula:

A S = ∬ D ∂ r ∂ u   × ∂ r ∂ v d u   d v

Beleza, então a primeira coisa que iremos fazer é achar as derivadas parciais de acordo com a fórmula acima. Depois iremos achar o produto vetorial entre elas.

Vamos dizer que

∂ r ∂ u   × ∂ r ∂ v = A

Mas cuidado, nós queremos achar a magnitude desse produto vetorial logo temos que fazer:

A = A x 2 + A y 2 + A z 2

Ai sim podermos substituir na integral mas antes de resolver ainda temos mais um passo que é encontrar novas coordenadas para a integral .Seria muito complicado encontrar os limites de integração sem fazer isso.

Vamos lá!

Passo 2

Bom , já sabemos que r ( u , v ) = ( u v , u + v , u - v ) , então precisamos achar as derivadas parciais ∂ r ∂ u e ∂ r ∂ v .

Vamos começar por ∂ r ∂ u :

∂ r ∂ u = ∂ ∂ u ( u v , u + v , u - v )

∂ ∂ u ( u v , u + v , u - v ) = ( v , 1,1 )

Agora para ∂ r ∂ v :

∂ r ∂ v = ∂ ∂ v ( u v , u + v , u - v )

∂ r ∂ v ( u v , u + v , u - v ) = ( u , 1 , - 1 )

Passo 3

Perfeito, já sabemos que:

∂ r ∂ u = ( v , 1,1 ) e ∂ r ∂ v = ( u , 1 , - 1 )

Agora vamos calcular o produto vetorial entre elas. Lembrando que um produto vetorial é calculado da seguinte forma: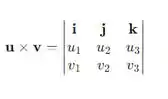

onde:

Montando nossa matriz temos que:

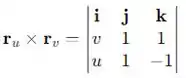
Logo :

u × v= i ( 1 . ( 1 ) - ( - 1 ) . 1 ) -   j ( u . ( 1 ) - ( - 1 ) . v ) -   k ( 1 . v - u . 1 ) )    

Assim podemos dizer que:

r u × r v = 〈 - 2 , u + v , v - u 〉

Passo 4

Agora vamos achar a magnitude, para isso vamos utilizar a fórmula:

A = A x 2 + A y 2 + A z 2

Lembra que eu chamei o resultado do produto vetorial de A só para simplificar, ok?

Então se A = r u × r v = 〈 - 2 , u + v , v - u 〉 .

Logo:

A = ( - 2 ) 2 + ( u + v ) 2 + ( v - u ) 2

Fazendo o produto notável:

A = 4 + u 2 + 2   u v + v 2 + u 2 - 2   u v + v 2

Logo:

A = 4 + 2 v 2 + 2 u 2

Passo 5

Vamos substituir os valores que encontramos na integral:

A S = ∬ D ∂ r ∂ u   × ∂ r ∂ v d A

Sabemos que:

∂ r ∂ u   × ∂ r ∂ v = 4 + 2 v 2 + 2 u 2

Logo:

A S = ∬ D 4 + 2 v 2 + 2 u 2 d A

Agora precisamos parametrizar em coordenadas polares visto que u 2 + v 2 ≤ 1 é a equação de um círculo de raio igual a 1, logo:

x = r   c o s   ( θ )

y = r   s e n   ( θ )

e

d A = r d r d θ

Esse valor é sempre o mesmo para coordenadas polares mas achamos através da fórmula:

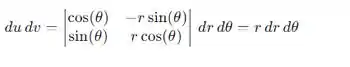
Beleza, agora que sabemos que as variáveis são r e θ , logo se queremos percorrer toda a circunferência:

0 ≤ r ≤ 1

e

0 ≤ θ ≤ 2 π

Vamos substituir na integral:

A S = ∬ D 4 + 2 v 2 + 2 u 2 d A

A S = ∫ 0 2 π ∫ 0 1 4 + 2 ( r s e n   θ ) 2 + 2 ( r   c o s θ ) 2 r d r d θ

A S = ∫ 0 2 π ∫ 0 1 4 + 2 r 2 s e n 2   θ + 2 r 2   c o s 2 θ r d r d θ

Um bizu muito bom é que normalmente quando temos s e n 2 θ   e   c o s 2   θ em um mesmo problema podemos tentar juntá los de tal forma para substituir por s e n 2 θ   +   c o s 2   θ = 1 .

Se colocamos o 2 r 2 em evidência temos que:

A S = ∫ 0 2 π ∫ 0 1 4 + 2 r 2 ( s e n 2 θ   +   c o s 2   θ ) r d r d θ

Assim:

A S = ∫ 0 2 π ∫ 0 1 r 4 + 2 r 2 d r d θ

Passo 6

Finalmente podemos resolver a nossa integral, lembrando começamos sempre da ordem de dentro para fora, ou seja, vamos começar resolvendo:

    ∫ 0 1 r 4 + 2 r 2 d r

Vamos utilizar o método de substituição:

4 + 2 r 2 = u

d t   u ' = d u

d t   ( 4 r ) = d u

d t   = d u 4 r

Substituindo na integral:

    ∫ 0 1 r u   d u 4 r

Logo:

    1 4 ∫ 0 1 u   d u

1 4 2 3 u 3 2 0 1

Substituindo mais uma vez 4 + 2 r 2 = u e passando o termo constante para fora.

2 12 ( 4 + 2 r 2 ) 3 2 0 1

1 6 ( 4 + 2 . 1 ) 3 2 - ( 4 + 2 . 0 ) 3 2

1 6 ( 6 ) 3 - ( 4 ) 3

Logo:

  ∫ 0 1 r 4 + 2 r 2 d r = 1 6 6 6 - 8

Substituindo em:

A S = ∫ 0 2 π ∫ 0 1 r 4 + 2 r 2 d r d θ

A S = ∫ 0 2 π 1 6 6 6 - 8 d θ

Passo 7

Vamos para a última parte:

∫ 0 2 π 1 6 6 6 - 8 d θ

Vamos tirar a parte constante da integral:

6 6 -   8 6 ∫ 0 2 π d θ

Logo:

6 6 -   8 6 θ 0 2 π

6 6 -   8 6 2 π - 0

Logo

∫ 0 2 π 1 6 ( 6 ) - 2 d θ = π 6 6 -   8 3

Assim:

A S = π 2 6 - 8 3

Resposta

π 2 6 - 8 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule ∬ K f x , y , z d S sendo: i )f x , y , z = z 1 + 4 x 2 + 4 y 2 ;σ é a parte do paraboloide z = 1 - x 2 - y 2 que se encontra dentro do cilindro x 2 + y 2 ≤ 2 y .
Calcule ∬_K f (x , y , z) d S sendo:c ) f (x , y , z) = x^2 + y^2 ; sigma (u , v) = (u , v , u^2 + v^2) , u^2 + v^2 = 1 .
Calcule ∬_K f (x , y , z) d S sendo:f (x , y , z) = x y ; sigma (u , v) = (u - v , u + v , 2 u + v + 1) , 0 = u = 1 e 0 = v = u .
Calcule ∬_K f (x , y , z) d S sendo:d ) f (x , y , z) = y ; sigma (u , v) = (u , v , 1 - u^2) , 0 = u = 1 ; 0 = v = sqrt(u) .
Calcule ∬ K f x , y , z d S sendo: d )f x , y , z = x 2 + y 2 ;σ a superfície x 2 + y 2 + z 2 = 4 ,z ≥ 1 . (Fica entendido aqui que σ é a parametrização mais “natural” do conjunto dado).