Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.1 - Ex. 7

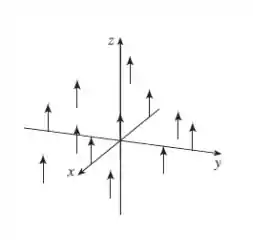
Esboce o campo vetorial , desenhando um diagrama como o da Figura ou da Figura .

Passo 1

Oi galera, tudo bem?

Nessa questão, precisamos esboçar um campo vetorial!

Pra isso, vamos olhar pra sua expressão de definição:

E ver como ela varia conforme os valores de e variam.

Com isso, vamos pegar alguns pontos e traçar os vetores de correspondentes.

Passo 2

Bom, o nosso campo é definido assim:

Esse represente a terceira coordenada, ou seja:

O valor da coordenada é porque .

O que a gente conclui com isso?

Esse campo vetorial é constante! Independente de quem é , o resultado vai ser , já que a definição do campo não depende de e :

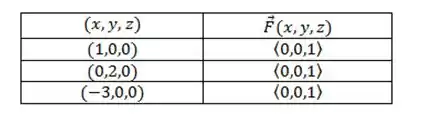
Esse vetor é um vetor que aponta na direção de , no sentido positivo, e tem tamanho .

Passo 3

Sabendo disso, vamos traçar o vetor em diversos pontos, pra representar o campo vetorial no :

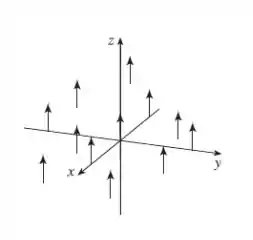
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

7. Determinar o trabalho realizado pela força conservativa f → = y z , x z , x y + 1 nos seguintes deslocamentos:(b) ao longo do arco de parábola x = y 2 - 1 , z = 2 , do ponto A(-1,0,2) ao ponto B(3,

8. Calcular ∫ C [ x x 2 + y 2 d x + y x 2 + y 2 d y ] , ao longo dos seguintes caminhos:(c) poligonal ABC com A(1,1), B(3,3) e C(4,1/4);

5. Calcular ∫ C f → ⋅ d r → , onde f → = y x 2 + y 2 , - x x 2 + y 2 , ao longo dos seguintes caminhos:d) circungerência de centro na origem e raio 4, no sentido anti-horário.

4. Verificar que as integrais são independentes do caminho de integração e determinar seus valores.g) ∫ 0,0 π , 1 e y c o s xd x + e y s e n xd y

5. Calcular ∫ C f → ⋅ d r → , onde f → = y x 2 + y 2 , - x x 2 + y 2 , ao longo dos seguintes caminhos:a) circunferência de centro em (4,4) e raio 2, no sentido anti-horário;