Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.1 - Ex. 9
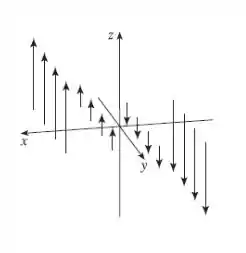
Esboce o campo vetorial , desenhando um diagrama como o da Figura ou da Figura .
Passo 1
E aii, pessoal?
Essa questão pede pra gente desenhar um diagrama que representa o campo vetorial
Pra isso, vamos ver como que esse campo se comporta conforme variamos o ponto . Também vamos calcular a norma, pra saber o tamanho do vetor, que calculamos assim:
Com essas informações, vamos desenhar alguns vetores resultantes do campo, e o diagrama que representa .
Passo 2
Olhando para a lei de definição do campo:
Esse representa a terceira coordenada, ou seja:
Calculando a norma:
Ou seja, pra um ponto , o vetor do campo é , que tem tamanho , então:
- Se , o vetor aponta para a direção positiva de
- Se , o vetor aponta para a direção negativa de
- Se , o campo é nulo:
Passo 3
Vamos fazer uma tabela com alguns valores de e os respectivos vetores nesses pontos:
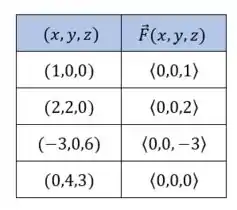
Então, o campo vetorial fica assim:
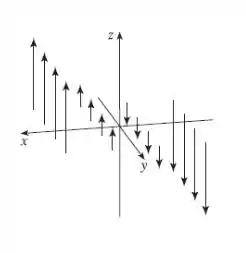
Resposta
Exercícios de Livros Relacionados
Verificar se o campo de forças f → é conservativo. Em caso afirmativo, determinar uma função potencial para esse campo e calcular o trabalho que ele faz sobre uma partícula que se desloca de A ( 1 , -
Verificar se o campo vetorial dado é conservativo. Em caso positivo, determinar uma função potencial para f → e o valor ∫ ( 0,0 , 0 ) ( a , b , c ) f → ⋅ d r → , onde a , b , c ∈R f → x , y , z = e x
Verificar se o campo vetorial dado é conservativo. Em caso positivo, determinar uma função potencial para f → e o valor ∫ ( 0,0 , 0 ) ( a , b , c ) f → ⋅ d r → , onde a , b , c ∈R f → x , y , z = x +
Calcular a integral ∫ C f → ⋅ d r → , onde f → é o campo vetorial dado, ao longo de qualquer caminho que une o ponto A ( 1,1 , 0 ) a B 1,2 - 1 . f → = 2 x 2 y + y 2 + z i ^ + 2 3 x 3 + 2 x y + z 2 j ^
26. Calcular a integral I = ∫ C [ x e x d x - ( x + 2 y ) d y ] , onde C é:a) o segmento de reta de ( 0,0 ) a ( - 1 , - 2 ) :