Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.6 - Ex. 1d

Determine o centro de massa da região A dada

d ) A = {(x , y) in R | x^2 <= y <= x}

Passo 1

Para encotrarmos o centro de massa precisamos achar x_c e y_c que são descritos por:

x_c = (int_a^b x [g (x) - f (x)] d x)/(Á r e a d e A)

y_c = (1)/(2) (int_a^b [g (x) + f (x)] [g (x) - f (x)] d x)/(Á r e a d e A)

A figura fica assim:

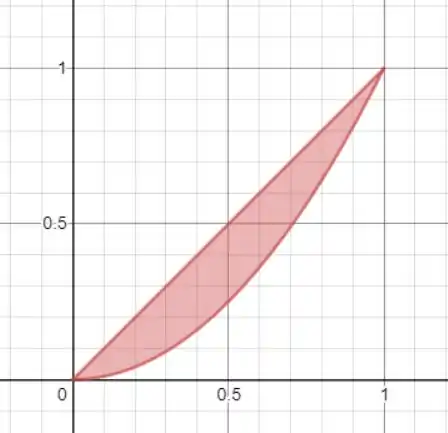
Daí vamos achar uma função y em função de x para calcular a área:

y (x) = [x - x^2]

Agora vamos achar a Área de A:

int_0^1 [x - x^2] d x

Vamos agora calcular.

Passo 2

int_0^1 [x - x^2] d x = [(x^2)/(2) - (x^3)/(3)] (1)/(0) = [(1)/(2) - (1)/(3)] = ((3 - 2)/(6)) = (1)/(6)

Agora que temos a Área de A vamos achar as outras integrais:

int_a^b x [g (x) - f (x)] d x = int_0^1 x [x - x^2] d x = int_0^1 [x^2 - x^3] d x = [(x^3)/(3) - (x^4)/(4)] (1)/(0) = ((1)/(3) - (1)/(4))

= ((4 - 3)/(12)) = (1)/(12)

int_a^b [g (x) + f (x)] [g (x) - f (x)] d x = int_0^1 (x + x^2) (x - x^2) d x

= int_0^1 (x^2 - x^4) d x = [(x^3)/(3) - (x^5)/(5)] (1)/(0) = ((1)/(3) - (1)/(5)) = ((2)/(15))

Passo 3

Agora substituímos:

x_c = (int_a^b x [g (x) - f (x)] d x)/(Á r e a d e A) = ((1)/(12))/((1)/(6)) = (1)/(2)

y_c = (1)/(2) (int_a^b [g (x) + f (x)] [g (x) - f (x)] d x)/(Á r e a d e A) = (1)/(2) ((2)/(15))/((1)/(6)) = (1)/(2) xx (12)/(15) = (2)/(5)

Resposta

(x_c , y_c) = ((1)/(2) , (2)/(5))

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Verificar se o resultado das seguintes integrais é postivo, negativo ou zero, sem calculá-las ∫ 0 2 π s e n t d t
Sem calcular a integral, verificar as seguintes desigualdade: ∫ π / 2 3 π / 2 - c o s x d x ≥ 0
∫ - 2 5 | 2 t - 4 | d t
∫ 0 4 | x 2 - 3 x + 2| d x
∫ 0 4 4 x 2 + 9 d x