Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 44

Determine o centro de massa do tetraedro sólido com vértices ( 0 ,   0 ,   0 ) ,   ( 1 ,   0 ,   0 ) ,   ( 0 ,   2 ,   0 ) ,   ( 0 ,   0 ,   3 ) e função densidade ρ x , y , z = x 2 + y 2 + z 2 .

Passo 1

Fala, pessoal! Tudo firme?

A questão quer o centro de massa do tetraedro sólido com vértices

0 ,   0 ,   0 ,   1 ,   0 ,   0 ,   0 ,   2 ,   0 ,   0 ,   0 ,   3

e função densidade

ρ x , y , z = x 2 + y 2 + z 2

O centro de massa de um sólido e dado por:

x , - y , - z - = M y z m , M x z m , M x y m

Onde M são os momentos em torno de cada um dos eixos:

M y z = ∭ E x ρ x , y , z d V

M x z = ∭ E y ρ x , y , z d V

M x y = ∭ E z ρ x , y , z d V

E m é a massa do sólido:

m = ∭ B ρ x , y , z d V

Então, o que precisamos fazer aqui é encontrar os limites de integração dessas integrais e calculá-las da forma que já sabemos, “de dentro pra fora”!

Como a questão traz o símbolo:

Vamos computar o valor das integrais diretamente em calculadoras. Aí você pode usar sua calculadora tipo HP Prime ou softwares como WolframAlpha.

Vamos lá!

Passo 2

Chamemos nosso tetraedro de W :

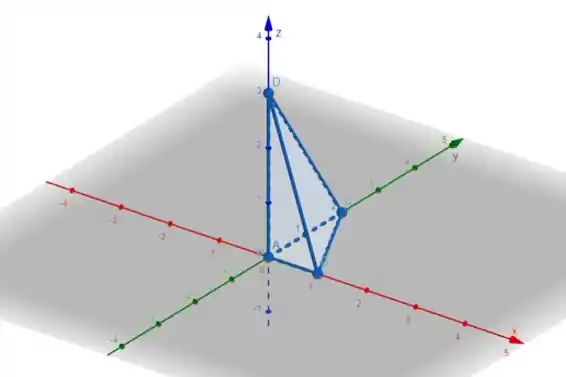
Precisamos determinar os limites de integração do nosso sólido

A face frontal de W é dada pelo plano:

x + y 2 + z 3 = 1  

Isolando z , temos:

  z = 3 - 3 x - 3 y 2

Como o sólido está totalmente acima do plano x y , ou seja, está somente na porção positiva do eixo z , temos:

0 ≤ z ≤ 3 - 3 x - 3 y 2

Para determinar os limites de x e y , precisamos olhar nosso sólido no plano x y :

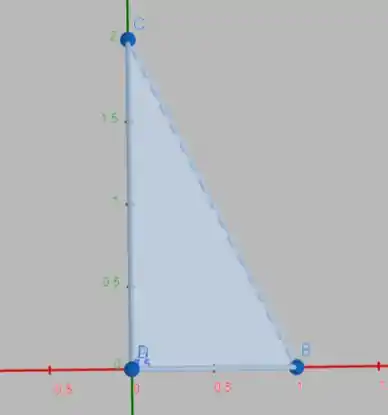
Podemos dizer que os limites de x são:

0 ≤ x ≤ 1

E para y , temos de zero até a reta que cruza o plano x y :

0 ≤ y ≤ 2 - 2 x

Passo 3

Agora que já temos nossos limites de integração podemos calcular nossas integrais. Então a massa total será dada por:

m = ∫ ∫ ∫ T ρ x , y , z   d V

Calculando no software, obtemos:

= ∫ 0 1 ∫ 0 2 - 2 x ∫ 0 3 - 3 x - 3 y 2 x 2 + y 2 + z 2   d z   d y   d x = 7 5

Passo 4

Como o valor da nossa massa, vamos procurar o valor do centro de massa. Vamos então calcular as integrais:

x - = M y z m = 1 m ∭ E x ρ x , y , z d V

y - = M x z m = 1 m ∭ E y ρ x , y , z d V

z - = M x y m = 1 m ∭ E z ρ x , y , z d V

Substituindo os valores de massa, da função ρ x , y , z e colocando os limites de integração, podemos obter pela calculadora:

x - = 5 7 ∫ 0 1 ∫ 0 2 - 2 x ∫ 0 3 - 3 x - 3 y 2 x x 2 + y 2 + z 2   d z   d y   d x = 4 21

y - = 5 7 ∫ 0 1 ∫ 0 2 - 2 x ∫ 0 3 - 3 x - 3 y 2 y x 2 + y 2 + z 2   d z   d y   d x = 11 21

z - = 5 7 ∫ 0 1 ∫ 0 2 - 2 x ∫ 0 3 - 3 x - 3 y 2 z x 2 + y 2 + z 2   d z   d y   d x = 8 7

Então:

x - , y - , z - = 4 21 , 11 21 , 8 7

Pronto, tá resolvido nosso problema!

Resposta

x - , y - , z - = 4 21 , 11 21 , 8 7

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Centro de massa, momento de inercia: encontre o centro de massa e o momento de inercia em relação ao eixo x de uma placa retangular fina delimitada pelas retas x = 0 , x = 20, y = - 1 e y = 1 se δ x ,
Encontrando um centroide: encontre um centroide da região do primeiro quadrante delimitado pelo eixo x, a parábola y 2 = 2 x e a reta x + y = 4 .
Centro de massa, momento de inércia: encontre o centro de massa e o momento de inercia em relação aos eixos coordenados e o momento de inercia polar de uma placa triangular fina delimitada pelas retas
Centroide de uma região infinita: encontre o centroide de uma região infinita no primeiro quadrante delimitada pelos eixos e pela curva y = e x . (Utilize integrais improprias nas formula de massa)
Encontre o centro de massa e o momento de inercia em relação ao eixo y de uma placa fina delimitada pela reta y = 1 e a parábola y = x 2 se a densidade for δ x , y = y + 1 .