Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 45

A função densidade conjunta das variáveis aleatórias X e Y é

f x , y = C x + y   s e   0 ≤ x ≤ 3 ,   0 ≤ y ≤ 2 0                                   c a s o   c o n t r á r i o

a Determine o valor da constante C

b Encontre P X ≤ 2 , Y ≥ 1

C Encontre P ( X + Y ≤ 1 ) .

Passo 1

E aí meus chuchus, tudo bom?

Nessa questão, foi nos dada uma função de densidade conjunta nas variáveis X e Y . Esse conceito foi explorado, no livro, na seção 15.5 (Aplicações das Integrais Duplas), nos Exemplos 6 e 7. Em resumo, se temos uma função de densidade conjunta, então a seguinte integral deve sempre valer 1:

∬ R 2 f x , y   d A = 1

Veja que R 2 é todo o plano x y . Porém, nossa função f x , y é limitada dentro do retângulo dado por:

R = x , y : 0 ≤ x ≤ 3   e   0 ≤ y ≤ 2

Vamos pra resolução!

Passo 2

  1. Para qualquer valor fora desse retângulo, nossa função vale 0 . Então, para calcular a integral acima, basta nos preocuparmos com os valores da função no retângulo 0,3 × 0,2 . Veja:

    2. ∬ R 2 f x , y   d A = ∫ 0 3 ∫ 0 2 C x + y   d y d x

    Calculando as integrais, temos que (lembrando que C é uma constante, assim ela pode sair das integrais):

    ∬ R 2 f x , y   d A = C ⋅ ∫ 0 3 x y + y 2 2 0 2 d x = C ⋅ ∫ 0 3 2 x + 2 d x

    ∬ R 2 f x , y   d A = C ⋅ x 2 + 2 x 0 3

    ∬ R 2 f x , y   d A = 15 C

    Ora, como vimos essa integral deve valer exatamente 1 . Dessa forma, conseguimos encontrar o valor da constante C :

    15 C = 1 ⟹ C = 1 15

    Passo 3

  2. Agora se tivermos P ( X ≤ 2 , Y ≥ 1 ) estamos dentro de um retângulo, conforme mostra a figura abaixo:

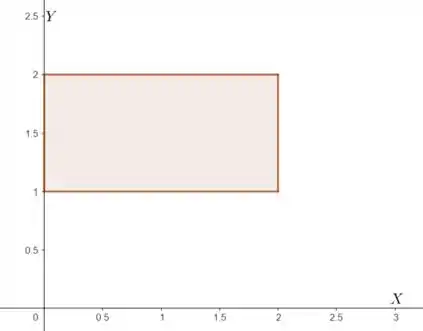
    3. Região de Integração

    P X ≤ 2 , Y ≥ 1 = ∫ - ∞ 2 ∫ 1 ∞ f x , y   d y   d x  

    P X ≤ 2 ,   Y ≥ 1 = ∫ 0 2 ∫ 1 2 1 15 x + y   d y d x

    Calculando a primeira integral, temos:

    ∫ 1 2 1 15 x + y   d y = 1 15 x y + y 2 2 1 2

    ∫ 1 2 1 15 x + y d y = 1 15 x + 3 2

    Assim, ficamos com:

    ∫ 0 2 1 15 x + 3 2   d x = 1 15 x 2 2 + 3 2 x 0 2 = 1 3

    Logo,

    P X ≤ 2 ,   Y ≥ 1 = 1 3

    Passo 4

  3. Para finalizarmos o problema vamos fazer o seguinte

P X + Y ≤ 1 = P X , Y ∈ D

Onde D é a região triangular mencionada no enunciado. Veja a figura abaixo

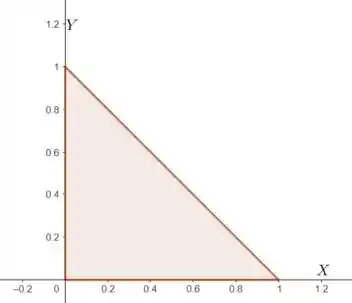
Região de integração

Podemos pensar numa região do tipo 1, onde temos x variando de 0 até 1 , enquanto o y varia de 0 até 1 - x (veja a figura abaixo):

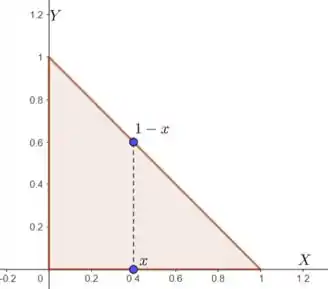
Região do tipo 1

P X + Y ≤ 1 = ∫ ∫ D f x , y   d A

P X + Y ≤ 1 = ∫ 0 1 ∫ 0 1 - x 1 15 ⋅ x + y   d y   d x

Resolvendo a primeira integral, temos:

∫ 0 1 - x 1 15 x + y   d y = 1 15 x y + y 2 2 0 1 - x = 1 15

P X + Y ≤ 1 = 1 15 ⋅ ∫ 0 1 x ⋅ 1 - x + 1 - x 2 2 d x

P X + Y ≤ 1 = 1 30 ⋅ ∫ 0 1 1 - x 2 d x

P X + Y ≤ 1 = 1 30 ⋅ x - x 3 3 0 1

Logo, temos que:

P X + Y ≤ 1 = 1 45

Pronto, tá resolvido mais uma questãozinha.

Resposta

a 1 15  

b   1 3

c 1 45

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja A o retângulo 1 = x = 2 , 0 = y = 1 . Calcule ∬_A f (x , y) d x d y , sendo f (x , y) igual a :c) sqrt(x + y)
Seja A o retângulo 1 = x = 2 , 0 = y = 1 . Calcule ∬_A f (x , y) d x d y , sendo f (x , y) igual a :y e^(x y)
Seja A o retângulo 1 = x = 2 , 0 = y = 1 . Calcule ∬_A f (x , y) d x d y , sendo f (x , y) igual a :h) (1)/((x + y)^2)
Seja A o retângulo 1 = x = 2 , 0 = y = 1 . Calcule ∬_A f (x , y) d x d y , sendo f (x , y) igual a :b ) x - y
Seja A o retângulo 1 = x = 2 , 0 = y = 1 . Calcule ∬_A f (x , y) d x d y , sendo f (x , y) igual a:m) (1)/(1 + x^2 + 2 x y + y^2)