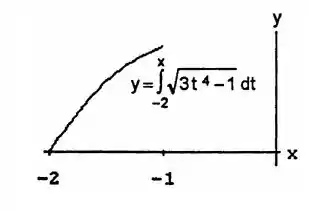Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.3 - Ex. 10
Determine o comprimento das curvas. Se tiver um programa gráfico, talvez queira esboçar o gráfico dessas curvas para ver como elas são
Passo 1
Para calcularmos o comprimento da curva, devemos usar a fórmula para o comprimento.
Como temos uma função de , a fórmula vai ser:
Entao precisamos de duas coisas, o intervalo de intergração, que ele deu no enunciado, e a derivada da , que é a função do enunciado.
O intervalo é de até , vamos para a derivada.
Para derivar, vamos usar o teorema fundamental do cálculo, encontramos:
Passo 2
Vamos para a interal do comprimento agora, usando oque achamos:
O valor de sempre vai ser positivo no intervalo de integração, podemos cortar aquele expoente com aquele quadrado sem necessidade de colocar o módulo
Cortando a raiz com o
Passo 3
Vamos resolver essa integral:
Primeiro, vamos ver a integral indefinida:
Passo 4
Voltando para a nossa integral definida:
Passo 5
Segue o gráfico dessa função para enxergamos como ela é:
