Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.7 - Ex. 1m

Desenhe a curva a seguir utilizando coordenadas polares

² = tg() , 0 π 2 ()

Passo 1

Primeiramente, devemos achar a função que demonstra como o varia com o Logo, isolando-se o temos:

Passo 2

Podemos então montar uma tabela com valores de e os correspondentes raios, para analisar o comportamento da função. Observe que para um ângulo de , o valor do raio tende ao infinito, uma vez que a tangente é a relação do seno (que vale 1 neste caso) dividido pelo cosseno (que vale 0 nesse caso).

Como a função está definida nos intervalo intervalos [0;e, podemos pegar o primeiro e rebater no terceiro quadrante, devido a simetria.

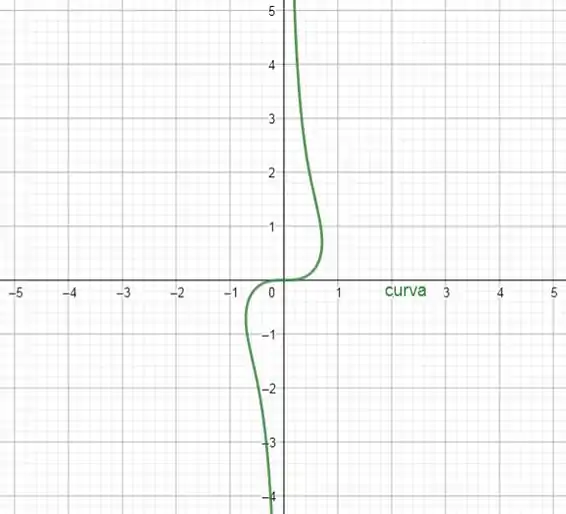
Passo 3

Ligando-se os pontos principais e sabendo-se que o raio tende ao infinito a medida em que teta se aproxima de , obtemos o gráfico abaixo:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o comprimento do arco da curva 8 y = x 4 + 2 x - 2 do ponto onde x = 1 até o onde x = 2 .

Use o Teorema 6.3.3 para encontrar o comprimento do arco da curva y 3 = 8 x 2 do ponto ( 1 ,2 ) ao ponto ( 27 ,18 ) .

Calcule o comprimento do segmento de reta x + 3 y = 4 do ponto ( - 2 ,2 ) ao ponto ( 4 ,0 ) por três métodos: (a) use a fórmula da distância. (b) use o Teorema 6.3.2. (c) use o Teorema 6.3.3.

Ache o comprimento do arco da curva y = 1 3 x ( 3 x - 1 ) do ponto onde x = 1 ao ponto onde x = 4 .

Calcule o comprimento do segmento de reta y = 3 x do ponto ( 1 ,3 ) ao ponto ( 2 ,6 ) por três métodos: (a) use a fórmula da distância. (b) use o Teorema 6.3.2. (c) use o Teorema 6.3.3.