Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.7 - Ex. 2d
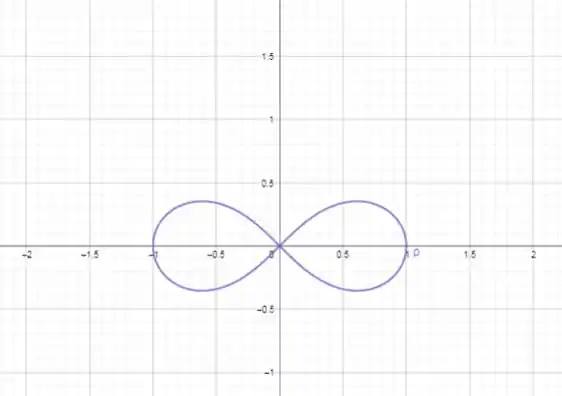
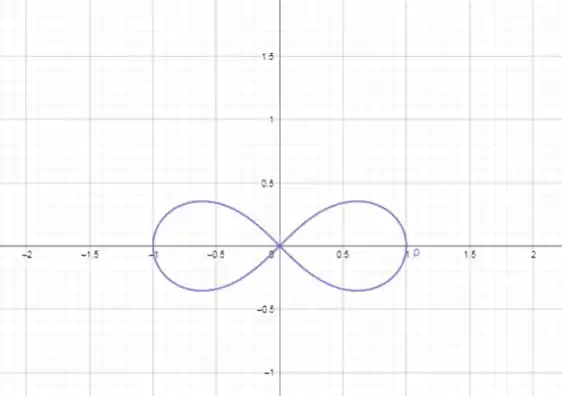
Passe a curva para coordenadas polares e desenhe-a:
(x²+y²)² = x² - y²
Passo 1
Sabemos que:
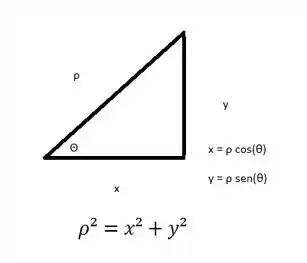
Logo:
(x²+y²)² = 4
x² - y² =
Igualando e cortando o
= cos(2
Passo 2
Para fazermos o gráfico, utilizaremos uma tabela de valores da função:
Destaque para o valor de π / 2 que não pertence ao domínio da função.
Passo 3
Podemos ligar os pontos acima para construir o gráfico:
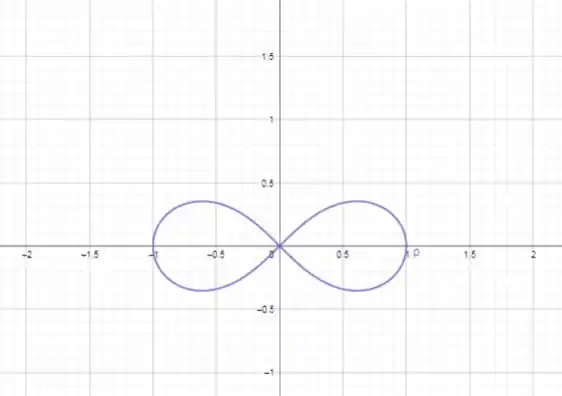
Resposta
cos(2 =
Exercícios de Livros Relacionados
Ache o centróide da região limitada pela parábola y 2 = x e pela reta y = x - 2 .
Ache o centróide da região limitada acima pela parábola 4 x 2 = 36 - 9 y e abaixo pelo eixo x .
Ache o centróide da região limitada pela parábola y = x e pela reta y = x 2 .
Ache o centroide da região no primeiro quadrante, limitadas pelos eixos coordenados e pela parábola y = 9 - x ² ²
Ache o comprimento do arco da curva 9 y 2 = 4 x 3 da origem ao ponto 3 ,2 3 .