Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.3 - Ex. 30
Determine se o conjunto dado é ou não: (a) aberto, (b) conexo e (c) simplesmente conexo.
Passo 1
E aii, pessoal, tudo certo?
Essa questão deu pra gente um conjunto:
E pediu pra gente verificar se ele é aberto, conexo e simplesmente conexo.
Tá... mas o que é isso?
Bora rever essas definições:
- Aberto: para todo ponto do conjunto existe uma bola aberta centrada nesse ponto que esteja inteira no conjunto.
- Conexo: quaisquer dois pontos no conjunto podem ser ligados por um caminho inteiro dentro do conjunto.
- Simplesmente conexo: é conexo, e qualquer curva fechada contorna só pontos que estejam dentro do conjunto.
Na prática, quer dizer que as curvas que limitam o conjunto não pertencem a ele:
Na prática, o conjunto não é constituído de dois ou mais pedaços separados.
Na prática, além de ser conexo, não tem nenhum buraco no conjunto.
Pra gente conseguir conferir essas classificações, a primeira coisa vai ser desenhar nosso conjunto no , e ai comparamos com as definições, uma a uma.
Passo 2
Nosso conjunto é
Basicamente é todo o , menos a reta , que é o eixo :
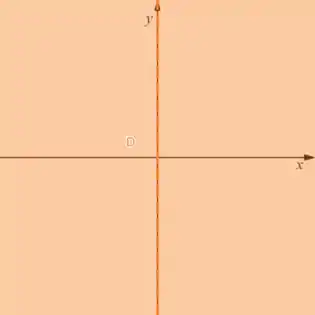
Passo 3
(a)
Essa não é tão trivial de analisar..., mas vamos pensar nesse conjunto como duas regiões separadas: à direita do eixo e à esquerda. O eixo é o limite das duas, e é a única curva que limita o conjunto. Como ele não faz parte de :
Sim, o conjunto é aberto.
Passo 4
(b)
Na letra a (a) gente já respondeu essa né? 😅
Nosso conjunto é dividido em duas partes desconectadas: uma delas é o primeiro e quarto quadrantes, e a outra é o segundo e terceiro. Ou seja,
Não, o conjunto não é conexo.
Passo 5
(c)
Aqui nem tem muito o que pensar – pra ser simplesmente conexo precisa antes de mais nada ser conexo, então:
Não, o conjunto não é simplesmente conexo.
Resposta
- Sim
- Não
- Não