Determine se o conjunto dado é ou não: (a) aberto, (b) conexo e (c) simplesmente conexo.
Passo 1
Faaala, galera!
Nessa questão, nós temos um conjunto
E precisamos determinar se ele é aberto, conexo e simplesmente conexo.
Pra isso, vamos relembrar essas definições:
- Aberto: para todo ponto do conjunto existe uma bola aberta centrada nesse ponto que esteja inteira no conjunto.
- Conexo: quaisquer dois pontos no conjunto podem ser ligados por um caminho inteiro dentro do conjunto.
- Simplesmente conexo: é conexo, e qualquer curva fechada contorna só pontos que estejam dentro do conjunto.
Na prática, quer dizer que as curvas que limitam o conjunto não pertencem a ele:
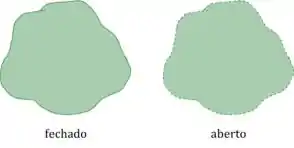
Na prática, o conjunto não é constituído de dois ou mais pedaços separados.
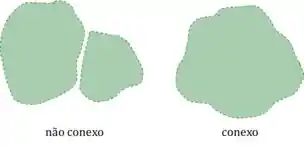
Na prática, além de ser conexo, não tem nenhum buraco no conjunto.
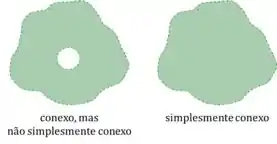
Então, a gente vai começar desenhando o nosso conjunto no , pra conseguir comparar com essas definições que acabamos de ver!
Daí vemos uma por uma se nosso conjunto se encaixa ou não nas definições.
Bora lá!
Passo 2
Nosso conjunto é
Ou seja, estamos no primeiro quadrante (já que e são positivos), e os eixos cartesianos não estão incluídos, porque e são estritamente maiores que .
Então:
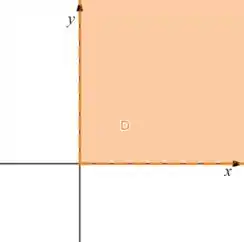
Passo 3
(a)
As curvas que limitem o nosso conjunto são os próprios eixos cartesianos: e . Como já vimos, o conjunto não inclui esses eixos, ou seja,
Sim, o conjunto é aberto.
Passo 4
(b)
A gente pode ver pelo desenho que nosso conjunto é o próprio primeiro quadrante, só não inclui os eixos. Isso quer dizer que ele é um conjunto de um pedaço só, não é dividido, então:
Sim, o conjunto é conexo.
Passo 5
(c)
Por fim, vemos que o conjunto não tem nenhum buraco, ele é formado pelo primeiro quadrante por inteiro, ou seja, além de ser conexo:
Sim, o conjunto é simplesmente conexo.
Resposta
- Sim
- Sim
- Sim