Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.2 - Ex. 33

Determine o conjunto de pontos nos quais a função é contínua.

G x , y = x + 1 - x 2 - y 2

Passo 1

Olá, meu brother. Vamos resolver essa atividade hoje?

Nós somos convocados aqui a determinar o conjunto de pontos para os quais a função:

G x , y = x + 1 - x 2 - y 2

É continua.

Uma função é dita continua se:

lim x , y → ( a , b ) ⁡ f x , y = f a , b

Mas não precisamos calcular o limite de todas as funções para encontrarmos seus pontos de continuidade, podemos analisar o seu domínio e identificarmos pontos de descontinuidade, onde a função não está definida.

Para encontrar o maior conjunto no qual G ( x , y ) é continua, para olhar para onde G ( x , y ) não está definida em R 2 .

Passo 2

Temos

G x , y = x + 1 - x 2 - y 2

Sabemos que dentro de raiz não podemos ter número negativo, logo temos duas raízes, isso nos diz que:

x ≥ 0

E

1 - x 2 - y 2 ≥ 0

Implicando que, nesse caso,

x 2 + y 2 ≤ 1

Logo, G ( x , y ) é continua no intervalo { ( x , y ) | x ≥ 0 ,   x 2 + y 2 ≤ 1 }

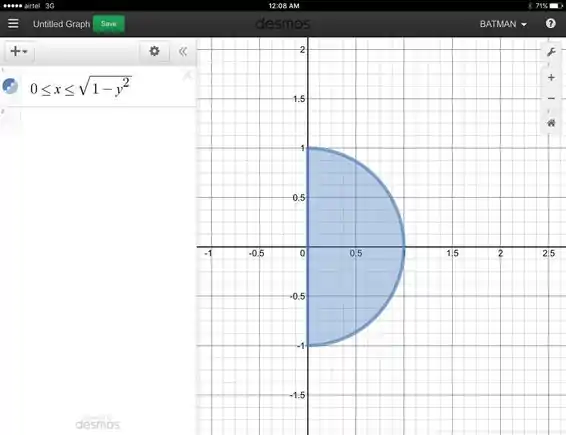
Abaixo podemos ver o gráfico da região de continuidade da nossa função:

Resposta

é contínua no intervalo { ( x , y ) | x ≥ 0 ,   x 2 + y 2 ≤ 1 }

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

22.Verificar se as funções dadas são contínuas nos pontos indicados:i) f x , y = x 2 + y 2 - 1 x + y ,P 1,1eQ ( 0,0 )
23. Escrever o conjunto em que a função dada é contínua:a) f x , y = x 2 y - x 3 y 3 - x 4 y 4
24. Calcular o valor de a para que a função dada seja contínua em (0,0):b) f x , y = x 2 y 2 y 2 + 1- 1 a - 4( x , y ) ≠ ( 0,0 ) x , y = ( 0,0 )
23. Escrever o conjunto em que a função dada é contínua:b) f x , y = x - 2 ( x y - 2 x - y + 2 ) ( y + 1 )
22.Verificar se as funções dadas são contínuas nos pontos indicados:b) f x , y =x 2 - y x x 2 - y 2 ,x≠ ±y 1 4 x + y , x = ±y,P ( 1,1 )