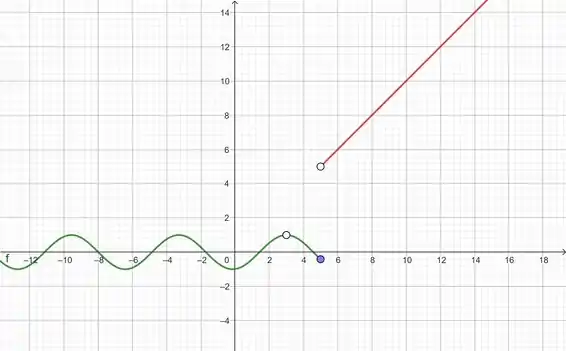
7. Esboce o gráfico de uma função que seja continua exceto para a descontinuidade declarada.
Descontinuidade removível em 3, descontinuidade com salto em 5
Passo 1
E ai meu parceiro? Pronto para mais uma resolução no padrão de qualidade que você já conhece?
Veja bem, aqui a gente quer encontrar uma função que não é continua em apenas um ponto. Que é o que nos foi dito no enunciado. Mas antes de tudo, o que é uma função continua?
Uma função continua tem os seguintes critérios atendidos:
1. está definido.
2. O limite de quando se aproxima de a partir de ambos os lados é igual a . Matematicamente, isso é expresso como:
3. A função está definida para todos os pontos em um intervalo aberto em torno de .
Já as descontinuidades removíveis podem ser "corrigidas" atribuindo um valor específico à função no ponto de descontinuidade, enquanto as descontinuidades de salto representam mudanças abruptas na função de um valor para outro em um ponto específico.
Graficamente, uma descontinuidade de salto parece uma mudança abrupta na função de um valor para outro em um ponto específico, sem qualquer possibilidade de preenchimento de lacuna.
Graficamente, uma descontinuidade removível parece uma "lacuna" na função que pode ser preenchida com um único ponto para tornar a função contínua nesse ponto.
Então a estratégia aqui é criar uma função definida por várias equações.
Passo 2
Primeiro vamos ter então a equação:
Pois precisamos de um salto em e aqui é, pois, em irei adicionar uma descontinuidade removível. Isso quer dizer que o limite da função neste ponto existe, porém o valor da função neste ponto não está definido.
Já em relação a descontinuidade de salto, eu aqui irei utilizar a equação:
Aqui a gente tem um pulo na definição da função, a gente tem um salto. O gráfico do que fizemos está abaixo. O mais importante aqui é entender a ideia por trás, existem diversas combinações de funções que podem atender o que precisamos, apenas mostrei uma delas.
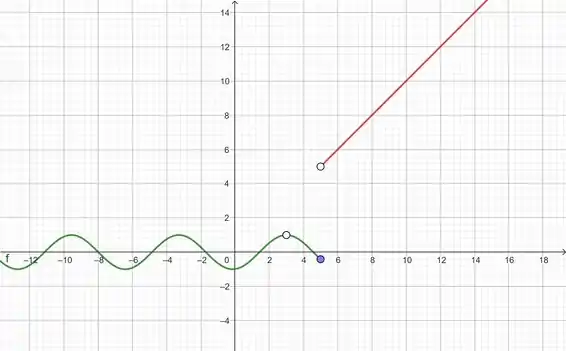
No final das contas, temos a nossa função definida por:
Resposta