Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 8f

Estude a variação de sinal de f ( x ) .

f (x) = (2 x - 3)/(1 - 2 x)

Passo 1

Primeiramente devemos achar as raízes ou os valores para os quais a função não está definida.

Como temos uma fração, e NÃO EXISTE divisão por zero, então o denominador deve ser não nulo, ou seja, 1 - 2 x != 0 => x != (1)/(2) mas mesmo excluindo esse ponto por conta de a função não estar definida nele devemos leva-lo em conta ao estudar o sinal da função.

Assim a única raiz de f é:

f (x) = 0

(2 x - 3)/(1 - 2 x) = 0

2 x - 3 = 0

x = (3)/(2)

Passo 2

Assim, podemos construir uma tabela analisando o sinal de cada termo da função e a respectiva divisão dos termos que gera f (x) :

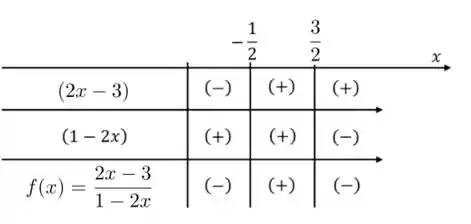
Assim, temos que:

f (x) > 0 para x in (- (1)/(2) , (3)/(2))

f (x) < 0 para x in (- oo , - (1)/(2)) uu ((3)/(2) , + oo)

Resposta

f (x) > 0 para x in (- (1)/(2) , (3)/(2))

f (x) < 0 para x in (- oo , - (1)/(2)) uu ((3)/(2) , + oo)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dê o domínio e esboce o gráfico.v ) y = sqrt(x^2)
Dê o domínio e esboce o gráfico.q ) y = | x | + (1)/(x)
Dê o domínio e esboce o gráfico. u ) y = | x |
Dê o domínio e esboce o gráfico.r ) y = sqrt(x - 1)
Dê o domínio e esboce o gráfico.s ) y = sqrt(x + 2)