Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 9m
Determine o dominio:
Passo 1
Oi pessoal, tudo bem? Vamos achar o domínio!
Para esboçar o domínio precisamos verificar se essa função tem alguma restrição para o valor de . Entre as restrições temos:
- O denominador em uma fração não pode ser zero
- O argumento de uma raiz par não pode ser menor que zero
- O argumento de uma função logarítmica não pode ser negativo
Então nos temos que verificar duas restrições! A do denominador e a da raiz.
Passo 2
Vamos começar pela primeira restrição: a do denominador não ser nulo.
Verificando qual valor que não pode assumir, temos
Além disso, temos uma raiz sexta que, assim como a raiz quadrada, não existe para numeros negativos, então devemos estudar o sinal da fração e excluir seus valores negativos. Temos então,
Agora vamos analisar essas informações juntas!
Passo 3
Assim, podemos construir uma tabela analisando o sinal de cada termo da fração:
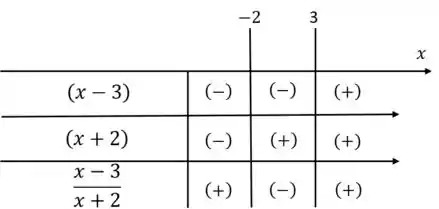
Vemos que se pegarmos um valor de entre e teremos um número negativo dentro da raiz, então devemos excluir os valores nesse intervalo. Assim, com temos o domínio: