Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 28a
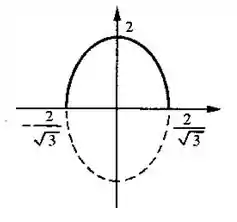
Determine o domínio e esboce o gráfico.
Passo 1
Oi, pessoal! Vamos começar achando o domínio. Para isso vamos ver se a função tem alguma limitação.
No caso temos uma raiz quadrada e como não podemos calcular raiz de número negativo, temos que o que ta dentro da raiz tem que ser maior ou igual a zero, ou seja,
Agora vamos resolver essa inequação e descobrir o domínio! Isolando ,
Podemos transformar tudo isso em positivo, mas temos que inverter o símbolo de maior ou igual tbm, fica assim
Calculando a raiz, temos
Temos que o domínio é:
Passo 2
O esboço do gráfico vai ter a cara de um polinômio de segundo grau, ou seja, uma parábola para baixo. Aqui temos o esboço do gráfico:
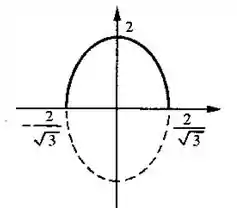
Resposta
Esboço do gráfico:
Exercícios de Livros Relacionados
Um ponto P no primeiro quadrante está na parábola y=x 2 . Expresse as coordenadas de P em função do ângulo de inclinação da reta que passa por P e pela origem.
Lei de Boyle: A Lei de Boyle diz que o volume V de um gás a uma temperatura constante aumenta sempre que a pressão P diminui, de modo que V e P são inversamente proporcionais. Se P = 14.7l b s / p o l
As variáveis r e s são inversamente proporcionais e r = 6 quando s = 4 . Determine s quando r = 10 .
Para que uma curva seja simétrica em relação ao eixo x , o ponto ( x , y ) deverá estar na curva se, e somente se, o ponto ( x , - y ) estiver na curva. Explique por que uma curva simétrica em relação
Determine uma janela de visualização apropriada para a função dada e a utilize para exibir o gráfico da função: y = 2 x - 3 x 2 / 3