Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 3
Um ponto P no primeiro quadrante está na parábola . Expresse as coordenadas de P em função do ângulo de inclinação da reta que passa por P e pela origem.
Passo 1
Fala, galeraa! Pra esse exercício, nós temos que lembrar que a inclinação de uma reta no plano cartesiano é dado por . O que ele quer é que você ache a equação dessa inclinação pra qualquer ponto e depois jogue na coordenada do ponto P(). Vou te mostrar como lá no Passo 2.
Passo 2
Olha como é o gráfico de no primeiro quadrante:
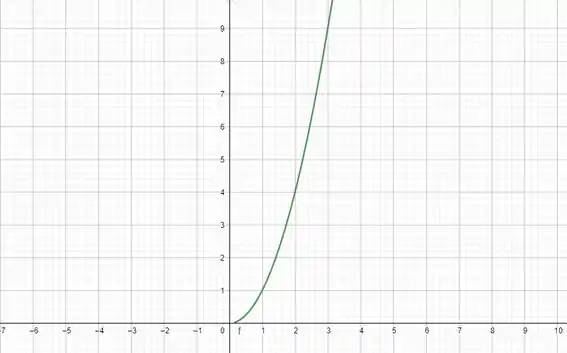
E quando a gente passa uma reta qualquer que pegue a origem e um ponto P qualquer fica assim:
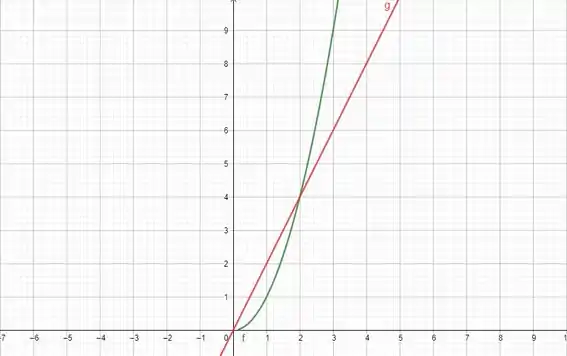
A inclinação dessa reta é dada por , onde é a distância, na reta , da origem até o ponto P e é a distância, na reta , da origem até o ponto P. Olha só como fica:
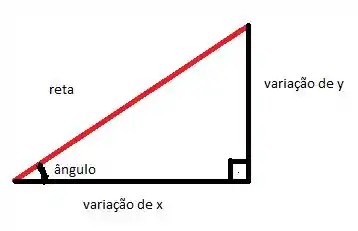
Repara de a tangente () também é . Então, a inclinação da reta é a mesma coisa que a tangente do ângulo. Pra essa função :
, porque, pra qualquer que eu pegar, o vai ser sempre .
Passo 3
Beleza. Nesse passo vamos achar o ponto P pra qualquer . Você concorda comigo que, pra qualquer que eu pegar, o vai ser sempre ? Então o nosso ponto P vai ser P() pra qualquer . Como, no Passo 2, a gente viu que, nesse caso, , onde tiver vamos jogar .
P() P(,), onde é o ângulo de inclinação da reta.
É só isso gente!
Resposta
P(,)