Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 37
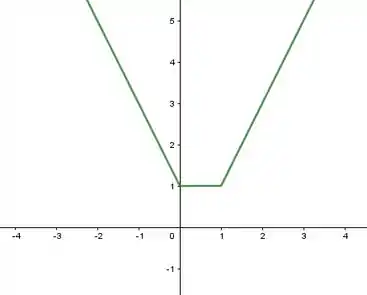
Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico.
Passo 1
Observe que é a soma do módulo de funções polinomiais. Como o domínio de uma função polinomial são os números reais, temos que o domínio de também será. Assim,
Passo 2
Como é a soma do módulo de funções polinomiais, temos que a sua imagem será todos os números reais, ou seja, .
Passo 3
Vamos fazer o estudos dos módulos que compõe .
Agora vamos analisar o comportamento de para cada intervalo de .
Logo, temos
Para fazer o gráfico de basta considerar cada um desses intervalos de e traçar as respectivas retas.
Resposta
Portanto, o domínio de é , a imagem é e o gráfico será dado por
Exercícios de Livros Relacionados
A figura a seguir mostra um retângulo inscrito em triângulo retângulo isósceles cuja hipotenusa tem 2 unidades de comprimento.Expresse a coordenada y de P em função de x . (Você pode começar escrevend
O gráfico da função mostra a altura da água na banheira como uma função do tempo . Dê uma descrição verbal do que você acha que aconteceu.
O gráfico mostra o consumo de energia por um dia em setembro em São Francisco . (P é medido em megawatts; t é medido em horas a partir da meia-noite). O que acontece com o consumo de energia às 6 da m
Três corredores competem em uma corrida de 100 metros . O gráfico representa a distância da corrida como uma função do tempo para cada corredor. Descreva o que o gráfico diz sobre essa corrida. Quem g
O gráfico mostra o consumo de energia por um dia em setembro em São Francisco . (P é medido em megawatts; t é medido em horas a partir da meia-noite). O que acontece com o consumo de energia às 6 da m