Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico.
Passo 1
Observe que a função apresenta uma raiz de ordem par, portanto é preciso garantir que a equação de dentro da raiz seja sempre não negativa. Inicialmente vamos determinar onde . Assim
Logo, teremos como solução
E também
Como é uma equação do segundo grau, e o coeficiente de é positivo, seu gráfico será uma parábola côncava para cima como na figura abaixo
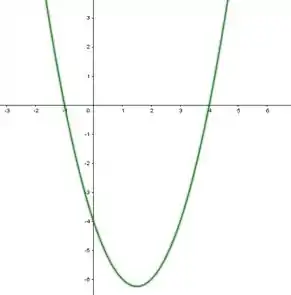
Assim, é não negativa (maior ou igual a zero) quando ou . Portanto o domínio de é .
Passo 2
Como é uma raiz de ordem par, sua imagem será todos os número reais não negativos, ou seja, .
Passo 3
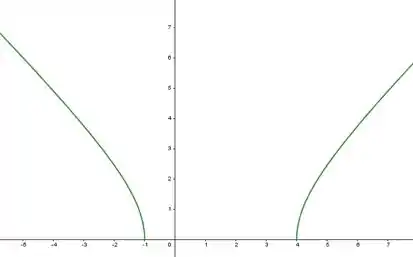
Observe que em temos um caso parecido com o exemplo 8 (p.42-43) do livro. Assim o gráfico de será semelhante ao do exemplo, porém partirá das raízes e .
Resposta
Portanto, o domínio de é , a imagem é e o gráfico será dado por