Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 79

Determine o domínio e a imagem de cada função composta. Em seguida, faça o gráfico das compostas em telas separadas. Os gráficos fazem sentido em cada caso? Justifique suas respostas e comente sobre as diferenças que você vê.

  1. y = s e n - 1 ( s e n x )
  2. y = s e n ( s e n - 1 x )

Passo 1

E aí, galera! Vamos lembrar, antes de mais nada, que s e n - 1   é a mesma coisa que a r c s e n , ou seja, o arco cujo seno vale determinada coisa.

Nosso passo-a-passo vai ficar assim:

  1. Achar o domínio e a imagem;
  2. Fazer o gráfico de cada função;
  3. Responder as perguntas.

Passo 2

LETRA A) y = s e n - 1 ( s e n x )

  1. Bom, vale lembrar que domínio são todos os valores possíveis para x e imagem são todos os valores de y que são ligados nos x .

    2. Para achar o domínio, vamos ver o que acontece com a s e n - 1 ( s e n x ) . Como o seno vai de -1 a 1, e o seno tá valendo s e n x (bugado, né?), temos que - 1 ≤ s e n x ≤ 1 . Pra quais valores de x o seno está entre -1 e 1? Todos!

    Então: D ( y ) = R

    A imagem vai ser os arcos que fazem s e n - 1 ( s e n x ) valer. Como não tem restrição pro que tá dentro do s e n - 1 , ele próprio vai poder ser qualquer arco que faz o seno variar de -1 a 1. Qual arco faz ele ser -1? O - π 2 . E qual faz ele ser 1? O π 2 . Então, a imagem vai de - π 2 até π 2 .

    Então: I m ( y )   =   [ - π 2 , π 2 ]

  2. O gráfico é assim:

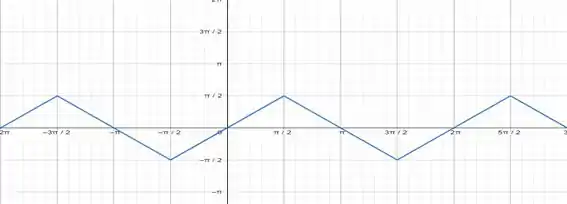
Passo 3

LETRA B) y = s e n ( s e n - 1 x )

  1. Para achar o domínio, vamos ver o que acontece com a s e n ( s e n - 1 x ) . O seno não tem restrições pro que tá dentro, então o s e n - 1 x pode ser qualquer número real. Então, se pode ser qualquer arco, o x ali dentro vai, necessariamente, de -1 a 1, que são os valores extremos pro seno.

Então: D ( y ) = [ - 1,1 ]

A imagem vai ser os arcos que fazem s e n ( s e n - 1 x ) valer. Como não tem restrição pro que tá dentro do s e n - 1 , ele próprio vai poder ser qualquer arco. Então, a imagem do seno que vale qualquer arco vai de -1 a 1, que são os extremos possíveis pra ele.

Então: I m ( y )   =   [ - 1,1 ]

(2) O gráfico vai ficar assim:

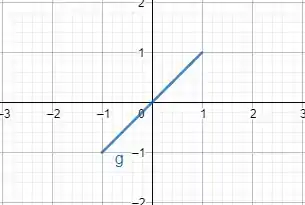
Passo 4

(3) Os gráficos fazem sentido?

Repara só:

O primeiro gráfico é de a r c s e n , que não é uma função periódica originalmente, ficou com o gráfico de uma função periódica. (Função periódica é aquela que se repete com um certo padrão)

Já o segundo gráfico é de seno, que é uma função periódica originalmente, mas seu gráfico não ficou periódico.

Então, eles não fazem sentido.

Resposta

  1. D ( y ) = R , I m ( y )   =   [ - π 2 , π 2 ] . O gráfico não faz sentido.
  2. D ( y ) = [ - 1,1 ] , I m ( y )   =   [ - 1,1 ] . O gráfico não faz sentido.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Expresse a equação: x = 5 3 s e n 2 π t + 5 2 c o s ⁡ ( 2 π t ) Na forma x = A s e n ( ω t + θ ) e use um recurso gráfico para confirmar que ambas as equações têm o mesmo gráfico.
Determine o número de soluções de x = 2 s e n ( x ) e use um recurso computacional ou gráfico para obter um valor aproximado dessas soluções.
9. Obtenha o gráfico da equação x^2 - 4 y^2 = 0 .
3. Um copo cheio de agua a uma temperatura de 11 ° C é colocado em uma sala que está á temperatura constante de 21 ° C . Faça um gráfico aproximado que descreva razoavelmente a temperatura da agua no
8. Denote por C o gráfico de y = 1 / x , para x0 .Expresse a distância entre o ponto P ( 1 ,0 ) e um ponto Q de C como uma função coordenada de x de Q .Qual é o dominio da função distância obtida em (