Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.1 - Ex. 64
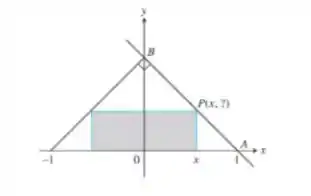
A figura a seguir mostra um retângulo inscrito em triângulo retângulo isósceles cuja hipotenusa tem 2 unidades de comprimento.
- Expresse a coordenada de em função de . (Você pode começar escrevendo uma equação para a reta AB).
- Expresse a área do retângulo em função de
Passo 1
Esta questão, a princípio, pode parecer complexa. Entretanto, ela somente é trabalhosa. O seu próprio enunciado nos fornece algumas dicas para que consigamos resolve-la. Então vamos começar a destrincha-lo. Observe primeiramente que o ponto está sobre a reta . Desta forma, as suas coordenadas satisfazem a equação da reta. Sendo assim, precisamos encontrar a equação da reta (ficou claro agora o porquê da sugestão da questão?) e para isto, precisamos determinar as coordenadas do ponto .
Após resolvermos a letra , nos sobra expressar a área do retângulo cinza. A área de todo retângulo é:
Como o nosso retângulo é simétrico em torno do eixo , o comprimento da sua base é:
Sendo um número pertencente ao intervalo . Já a altura do retângulo será o valor de encontrado na letra (faz sentido agora a ordem das perguntas?)
Passo 2
Vamos então seguir o procedimento descrito no Passo 1. Portanto, vamos descobrir qual a coordenada do ponto . De cara, podemos afirmar que , visto que o ponto está sobre o eixo . Nos falta então determinar quem é . Para isto, vamos descobrir qual o valor dos lados dos catetos do nosso triângulo retângulo isósceles. Por ser um triângulo isósceles, os seus catetos possuem um mesmo comprimento . Além disto, por ser retângulo, é válido o Teorema de Pitágoras. Portanto:
É importante lembrar que, como representa uma medida de comprimento, só é aceito valores positivos.
Passo 3
Para descobrirmos as coordenadas do ponto , vamos utilizar o comprimento descoberto anteriormente. Agora, precisamos calcular o valor da altura em relação a hipotenusa do triângulo. Veja só o seguinte recorte do nosso problema:
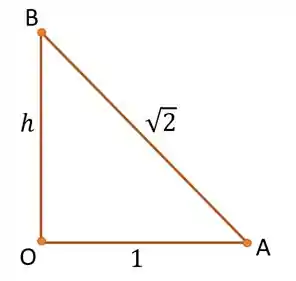
Para descobrir quem é , basta utilizarmos o Teorema de Pitágoras. Portanto:
Assim, as coordenadas do ponto são .
Passo 4
Temos agora todas os dados necessários para obter os coeficientes da reta que passam pelos pontos e . Vamos substituir as coordenadas destes pontos na equação da reta e resolveremos o nosso sistema de 2 equações e 2 incógnitas. Assim temos:
Da segunda equação obtemos que . Substituindo este valor na primeira, descobrimos que . Portanto, a equação da reta é:
E, a coordenada do ponto , o qual pertence também a reta , é
Passo 5
Agora que obtemos o valor da altura do retângulo em função do comprimento , basta substitui-lo na equação da área descrita no Passo 1. Portanto, obtemos: