Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 4
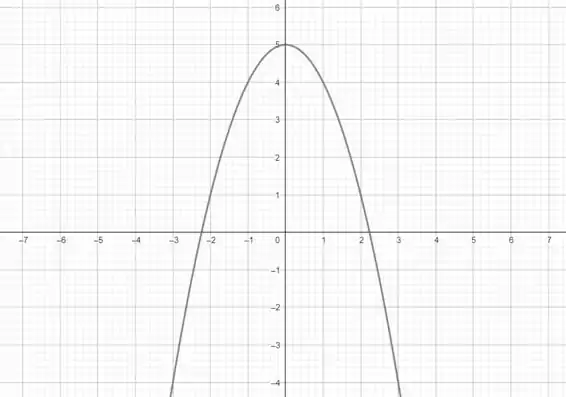
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Temos um polinômio do 2º grau! Já sabemos que ele está definido para todos os valores de e que seu gráfico é uma parábola! Vamos delimitar a imagem desse rapazinho a partir do que sabemos de equações quadráticas.
Passo 2
Para qualquer valor de :
Agora multiplicando os dois lados por e invertendo a inequação:
E agora somando 5 em ambos os lados:
O lado esquerdo da nossa equação é igual à nossa ! Então podemos escrever isso como:
Acabamos de definir a nossa imagem! E o limite do conjunto da imagem é o dito ponto de inflexão da parábola.
Passo 3
Agora vamos para o gráfico da . Sabemos que é uma parábola que está definida para todos os valores menores que . No gráfico isso fica:
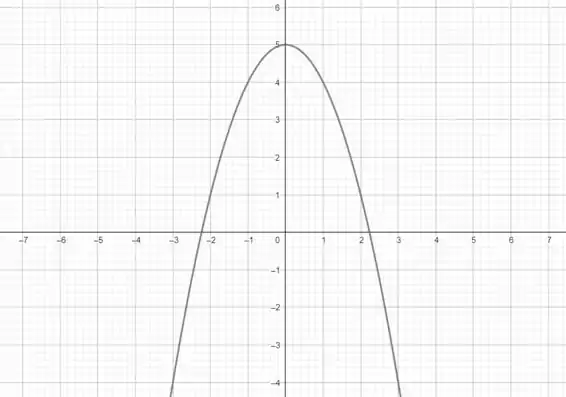
Resposta
Domínio:
Imagem:
