Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 6
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Vamos passo a passo com essa belezinha. Começando pelo domínio, depois a imagem e por último a gente usa o que temos para fazer o gráfico.
Passo 2
Para uma função que tem uma raiz, precisamos que o que está dentro da raiz seja não negativo. No nosso caso:
Agora é só isolar o e teremos a restrição do nosso domínio!
Esse intervalo define o nosso domínio:
Passo 3
Agora vamos pegar a nossa primeira linha do passo anterior:
Tirando a raiz quadrada dos dois lados:
Ou seja:
Então a imagem da fica:
Passo 4
Pra fechar o exercício precisamos do gráfico da função. Sempre que tivermos funções de raiz quadrada pense que temos meia parábola deitada. Se isolarmos o na equação:
Vamos fazer , só pra ficar mais fácil de manipular, show?
Agora sim vamos isolar o :
Agora temos a equação de uma parábola no eixo ! Mas repare que por conta da imagem da nossa função original, só vamos ficar com os valores de .
No gráfico isso fica:
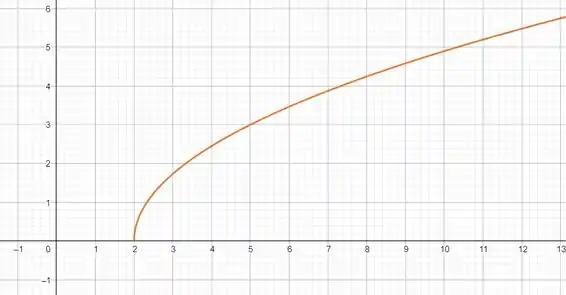
Resposta
Domínio:
Imagem:
