Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 15
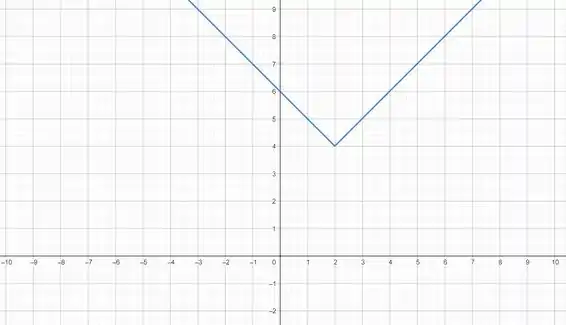
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Eu vou te passar uma dica show de bola pra plotar qualquer gráfico de um função modular num instante, saca só:
Se temos uma função do tipo
- Representa o deslocamento no eixo .
- Representa o deslocamento no eixo .
Fica facinho de plotar o gráfico e depois é só determinar o domínio e a imagem que é num instante. Imagina que estamos pegando a função módulo e transladando ela em unidades em e em unidades em . Quando a gente resolver o exercício vai ficar tudo mais tranquilo, vamos pro gráfico.
Passo 2
Na nossa função:
E
O ponto e define o vértice da nossa função módulo. É como se tivéssemos uma função modular , porém ela foi deslocada de . Então nosso gráfico fica assim:
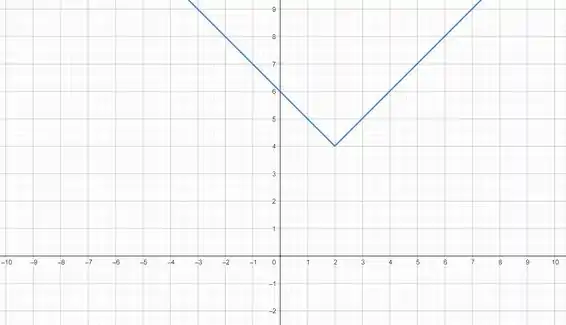
Passo 3
Olhando pro gráfico da função, temos que a as duas semirretas se estendem para todos os valores de , ou seja, nosso domínio é . E a imagem será todos os valores que pode assumir. Também olhando pro gráfico, podemos ver que o está definido para todos os valores maiores ou iguais a Entao a nossa imagem fica .
Resposta
Domínio:
Imagem:
