Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.3 - Ex. 66
- Determine uma equação para a reta que seja tangente à curva na origem.
- Esboce a curva e a tangente em um único gráfico. A tangente intercepta a curva em outro ponto. Use os comandos “Zoom” e “Trace” para estimar as coordenadas desse ponto.
- Confirme suas estimativas das coordenadas do segundo ponto de interseção resolvendo as equações da curva e da tangente simultaneamente (tecla “Solver”).
Passo 1
Para resolvermos a letra a.) precisamos encontrar a tangente à curva no ponto . Para isso, precisamos calcular o coeficiente angular da tangente a partir da derivada de :
Lembrando da equação da tangente:
Passo 2
O gráfico com a tangente e a curva podem ser vistos na figura abaixo:
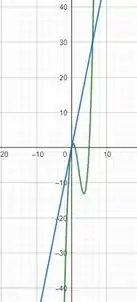
A tangente passa por outro ponto da curva . Olhando no gráfico, o ponto interceptado é .
Passo 3
Já na letra c.), a questão pede para estimarmos o ponto que a tangente intercepta a curva além do ponto de tangência. Assim, iremos igualar as duas funções:
Agora precisamos encontrar o valor de :
Pronto!!!
Resposta
Exercícios de Livros Relacionados
Calcule f ' x . f x = x 2 ln x + 2 e x
Seja f x = x 2 sen x + cos x . Calcule: f ' x f ' 0 f ' 3 a f ' x 2
46. a) Use uma calculadora para tabular até quatro casas decimais, valores de sec π 6 + h - sec π 6 h Quando hé0,1 ;0,01 ;0,001 ; 0,0001 ; 0,00001e é hé - 0,1 ;- 0,01 ;- 0,001 ;- 0,0001 ; é - 0,00
44. a) Use uma calculadora para tabular até quatro casas decimais, valores de c o s 5 π 6 + h - c o s 5 π 6 h Quando hé1 ;0,5 ;0,1 ;0,01 ;0,001 ;ehé- 1 ;- 0,5 ;- 0,1 ;- 0,01 ;- 0,001 é é . A que o quo
45. a) Use uma calculadora para tabular até quatro casas decimais, valores de t g π 4 + h - t g π 4 h Quando hé0,1 ;0,01 ;0,001 ; 0,0001 ; 0,00001e é hé - 0,1 ;- 0,01 ;- 0,001 ;- 0,0001 ; é - 0,00001