Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.7 - Ex. 1c

Determine a equação da reta tangente às seguintes curvas, nos pontos indicados. Esboçar o gráfico em cada caso.

f x = x 3 x - 5 ;       x = 1 2 ,         x = a ,         a ∈ R

Passo 1

Vamos lá, temos que a equação da reta tangente é da forma:

y - y 0 = m x - x 0

Onde x 0 , y 0 são pontos da reta, e m é a inclinação da reta que é igual a derivada de f x no ponto que queremos.

Temos que:

f x = x 3 x - 5 = 3 x 2 - 5 x

Vamos achar a inclinação:

m = f ' x 1 = lim ∆ x → 0 ⁡ f x 1 + ∆ x - f x 1 ∆ x =

= lim ∆ x → 0 ⁡ 3 x + ∆ x 2 - 5 x + ∆ x - 3 x 2 - 5 x   ∆ x =

= lim ∆ x → 0 ⁡ 3 x 2 + 2 x ∆ x + ∆ x 2 - 5 x - 5 ∆ x   - 3 x 2 + 5 x   ∆ x =

= lim ∆ x → 0 ⁡ 3 x 2 + 6 x ∆ x + 3 ∆ x 2 - 5 ∆ x   - 3 x 2   ∆ x = lim ∆ x → 0 ⁡ 6 x ∆ x + 3 ∆ x 2 - 5 ∆ x   -   ∆ x =

= lim ∆ x → 0 ⁡ 6 x + 3 ∆ x - 5 = 6 x + 3 ⋅ 0 - 5 = 6 x - 5

Passo 2

Para x = 1 2 vamos ter:

m = f ' 1 2 = 6 ⋅ 1 2 - 5 = 3 - 5 = - 2

E só nos falta achar f 1 2 :

f 1 2 = 3 ⋅ 1 2 2 - 5 ⋅ 1 2 = 3 ⋅ 1 4 - 5 2 = 3 - 10 4 = - 7 4

Vamos montar a equação:

y - y 0 = m x - x 0 → y - f 1 2 = f ' 1 2 x - 1 2 → y - - 7 4 = - 2 x - 1 2 →

y = - 2 x + 1 - 7 4 → y = - 2 x - 3 4

Passo 3

E por último, para x = a vamos ter:

m = f ' a = 6 a - 5

E só nos falta achar f a :

f a = 3 a 2 - 5 a

Vamos montar a equação:

y - y 0 = m x - x 0 → y - f a = f ' a x - a → y - 3 a 2 - 5 a = 6 a - 5 x - a →

y - 3 a 2 + 5 a = 6 a - 5 x - 6 a 2 + 5 a → y = 6 a - 5 x - 6 a 2 + 5 a + 3 a 2 - 5 a →

y = 6 a - 5 x - 3 a 2

Passo 4

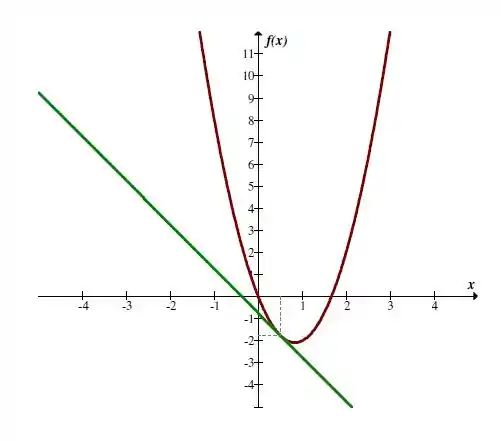
Aqui temos o gráfico da reta tangente para x = 1 2 :

Para x = a não podemos representar em um gráfico, pelo fato de a ser um valor genérico.

Resposta

y = - 2 x - 3 4

y = 6 a - 5 x - 3 a 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a derivada. y = t 3 t 2 + 1 2
Calcule a derivada. y = x 2 + 1 x + 1
Calcule a derivada. x = e t 2 s e n ( 3 t )
Calcule a derivada. y = ln ⁡ 1 + tg ⁡ x 2 1 - tg ⁡ x 2
Calcule a derivada. y = 2 4 + 3 x 3 2 - x 3 3 2 5