Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.7 - Ex. 3

Determine a equação da reta tangente à curva y = 1 - x 2 , que seja paralela à reta y = 1 - x . Esboçar os gráficos, da reta dada e da reta tangente encontrada.

Passo 1

Vamos lá, temos que a equação da reta tangente é da forma:

y - y 0 = m x - x 0

Onde x 0 , y 0 são pontos da reta, e m é a inclinação da paralela.

Passo 2

Como queremos que seja paralela à reta y = 1 - x , então vamos ter que o m da equação é:

m = - 1

Para achar o ponto vamos calcular f ' x :

f ' x 1 = lim ∆ x → 0 ⁡ f x 1 + ∆ x - f x 1 ∆ x = lim ∆ x → 0 ⁡ 1 - x + ∆ x 2 - 1 - x 2   ∆ x =

= lim ∆ x → 0 ⁡ 1 - x 2 - 2 x ∆ x - ∆ x 2 - 1 + x 2   ∆ x = lim ∆ x → 0 ⁡ - 2 x ∆ x - ∆ x 2   ∆ x =

= lim ∆ x → 0 ⁡ - 2 x - ∆ x = - 2 x - 0 = - 2 x

Vamos igualar a inclinação que acharmos com f ' x para encontrar o ponto:

m = - 1 → - 2 x = - 1 → x = 1 2

Passo 3

E só nos falta achar f 1 2 :

f 1 2 = 1 - 1 2 2 = 1 - 1 4 = 3 4

Vamos montar a equação:

y - y 0 = m x - x 0 → y - f 1 2 = m x - 1 2 → y - 3 4 = - 1 x - 1 2 →

y = - x + 1 2 + 3 4 → y = - x + 5 4

Passo 4

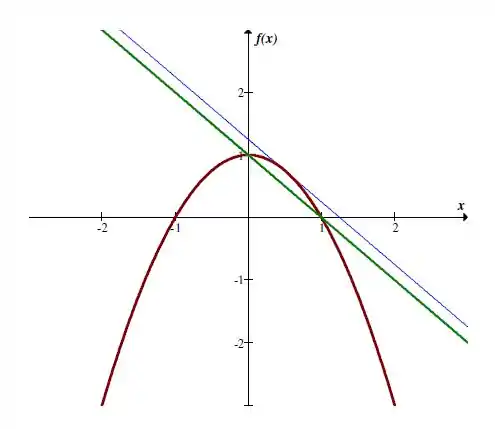
Esboçando os gráficos da reta dada, da reta tangente encontrada e da curva temos:

Resposta

y = - x + 5 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Derive a função dada, aplicando os teoremas desta seção.18. H x = 5 6 x 5
Calcule a derivada y = 1 + x
Calcule a derivada y = ln ⁡ 3 x + 1 + 9 x 2
Calcule a derivada y = x5 x 2
Calcule, pela definição, a derivada da função dada, no ponto dado. f x = e x 2 em p = 0