Seja σ a transformação do exercício anterior. Verifique que σ transforma o retângulo 0 ≤ u ≤ 1, 0 ≤ v ≤ 2π e w = 1, em um círculo. Desenhe tal círculo.
Passo 1
A transformação do exercício anterior é:
Bom, no caso desse retângulo, a gente tem o seguinte:
Ou seja, temos em :
Que é um círculo de raio , no caso variando de .
Como é fixo, temos um círculo de raio no plano . Eis o desenho:
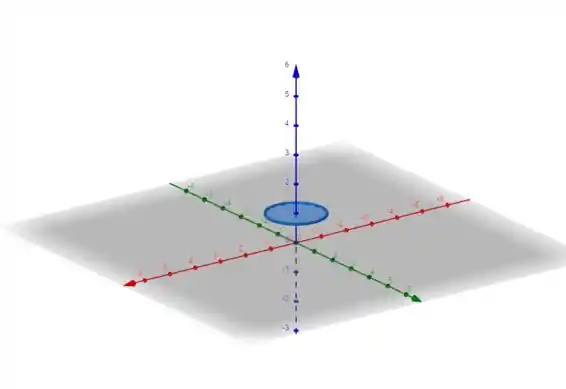
Resposta
Ei, a resposta está no passo a passo :)