Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.1 - Ex. 15
Considere a transformação σ (θ, ρ, φ) = (x, y, z) onde x = ρ sen φ cos θ, y = ρ sen φ sen θ e z = ρ cos φ.
- Desenhe σ (B) onde B é o conjunto ( constante), 0 ≤ θ ≤ 2π e 0 ≤ φ ≤ π.
- Desenhe σ (B) onde B é o paralelepípedo 0 ≤ ρ ≤ 1, 0 ≤ θ 2π e 0 ≤ φ ≤ π.
Passo 1
- Vamos lá, considerando as coordenadas esféricas, temos nesse caso:
- Bom, agora a gente tem uma variação em também, ou seja, nesse caso temos uma esfera de raio .
Podemos fazer então:
Ou seja, temos a superfície esférica de raio .
O desenho:
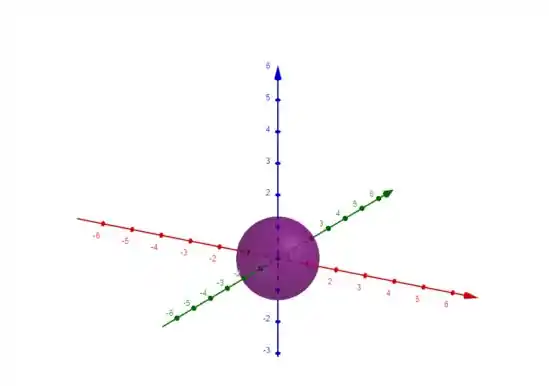
Passo 2
A equação aqui se torna:
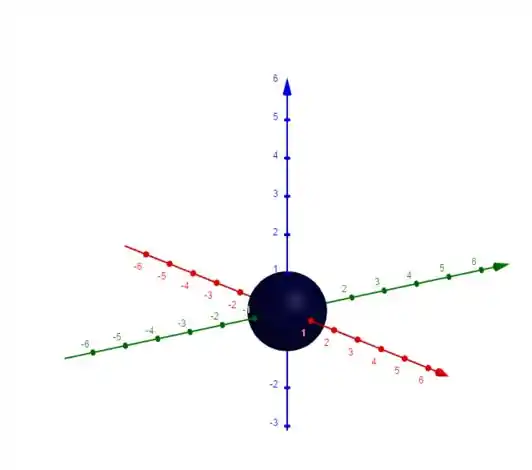
Se liga na diferença entre esfera e superfície esférica! Superfície esférica é só a “casca” da esfera. Esfera é tudo, roliço, tipo uma bola mesma. A diferença nas equações é o raio fixo ou o raio variando😉
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dadaA parte da esfera x 2 + y 2 + z 2 - 4 z = 0 que está acima do plano z = 2
Seja σ u , v = ( x , y , z ) , com x = u cos v , y = us e nv e z = u 2 . Mostre que σ transforma a faixa u ≥ 0 , 0 ≤ v ≤ 2 π , no paraboloide z = x 2 + y 2 .
Desenhe a imagem de σ u , v = u , v ,1 - u 2 - v 2 , com u 2 + v 2 ≤ 1 .
Desenhe a imagem de σ u , v = ( cos v ,s e nv ,u ) , com 0 ≤ u ≤ 1 e 0 ≤ v ≤ 2 π .
Seja σ u , v = ( x , y , z ) , com x = u cos v , y = us e nv e z = u .Mostre que a transformação σ transforma a reta u = u 1 ( u 1 ≠ 0 constante) numa circunferência. Desenhe tal circunferência no c