Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.1 - Ex. 22
Determine e esboce o domínio da função.
Passo 1
Fala ai galerinha! Tranquilo?
Vamos começar a questão montando uma estratégia de resolução. Se liga!
Primeiro vamos identificar a condição para a função estar definida em. Para isso precisamos reorganizar a inequação e verificar o padrão da equação comparando com uma curva já existente.
Partiu resolver?
Passo 2
Queremos determinar o domínio de . Ou seja, queremos saber que valores de ,z que podem ser usados para que seja real.
Para definir o domínio, é melhor olhar para as restrições.
Logo,
Separando os termos literais dos termos não literais
Simplificando
Passo 3
Logo, o domínio é definido por
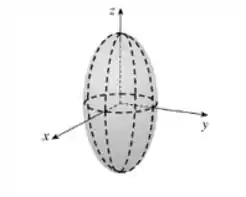
Trata-se dos pontos no interior do elipsoide , conforme a figura abaixo:
Resposta
Exercícios de Livros Relacionados
Cada um dos Exercícios 75-78 apresenta uma função f (x, y, z) e um número positivo ϵ . Em cada exercício, mostre que existe um δ 0 tal que, para todo número (x, y, z), x 2 + y 2 + z 2δ ⇒ f x , y , z -
Nos Exercícios 1-4, encontre o domínio e a imagem da função dada e identifique suas curvas de nível. Esboce uma curva de nível típica. f x , y = 9 x 2 + y 2
Nos Exercícios 1-4, encontre o domínio e a imagem da função dada e identifique suas curvas de nível. Esboce uma curva de nível típica. g x , y = x 2 - y
Nos Exercícios 5-8, encontre o domínio e a imagem da função dada e identifique suas superfícies de nível. Esboce uma curva de nível típica. k x , y , z = 1 x 2 + y 2 + z 2 + 1
Nos Exercícios 1-4, encontre o domínio e a imagem da função dada e identifique suas curvas de nível. Esboce uma curva de nível típica. g x , y = 1 x y