Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.1 - Ex. 21
Determine e esboce o domínio da função.
Passo 1
Fala, meu parceirooo. Vamos resolver essa atividade aqui, pode ficar tranquilo que hoje você sai daqui com todas as dúvidas sanadas.
Temos a função:
Queremos determinar o domínio de . Ou seja, queremos saber que valores de ,z que podem ser usados para que seja real.
Para definir o domínio, é melhor olhar para as restrições. Cada função tem suas restrições, e no caso da função raiz, a gente não pode ter valores negativos dentro das raízes, então é nisso que iremos trabalhar para encontrar qual o conjunto de valores que podem fazer parte da nossa função.
Passo 2
Como não podemos ter valores negativos dentro da nossa função, teremos então a restrição:
Logo, o domínio é definido por
Trata-se de uma esfera centrada em e de raio 1, conforme mostrado na figura abaixo:
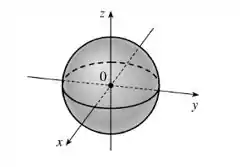
Então o que está dentro e na fronteira da nossa esfera faz parte do nosso domínio.