Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.3 - Ex. 12
Determine e e faça o gráfico de e com domínios e pontos de vista que permitam ver a relação entre eles.
Passo 1
Opa, tudo belezinha? Questãozinha de derivadas parciais, vamos lá!
A questão nos dá uma função e pede as derivadas parciais e . Além disso, a questão também pede para a gente plotar os gráficos dessas derivadas!
Pra encontrar as derivadas parciais é mole: Nós fixamos as variáveis que não estão envolvidas na derivação como constantes e derivamos normal! Por exemplo, se quisermos derivar em , nós tratamos como um número qualquer.
Então a gente vai fazer esse processo pra encontrar as duas derivas e depois plotar o gráfico!
Passo 2
Vamos começar encontrando , para isso tratamos como constante, de forma que:
Para encontrar a derivada dessa função podemos usar a regra do produto!
Relembrando:
A regra do produto nos diz que para uma função
A sua derivada é dada por
Dessa forma
Onde o resultado da derivada
Pode ser encontrado usando a regra da cadeia!
Relembrando:
A regra da cadeia nos diz que para uma função
A sua derivada é dada por
De forma que:
Com essas informações conseguimos chegar em
Agora vamos encontrar a derivada em
Mas observe que, como é constante durante o cálculo dessa derivada, temos o seguinte
E essa derivada nós acabamos de calcular para ! De forma que:
Passo 3
Para plotar o gráfico temos algumas opções. Idealmente, para esse tipo de questão, o MATLAB é a melhor opção. No entanto, além de ser um software pago, ele também é um programa bem pesado.
Ai que entra o GeoGebra, nossa opção gratuita e que roda no navegador! Basta entrar no site (geogebra.org/calculator) e digitar as funções no campo “Calculadora 3D”
Começando pelo gráfico de visto pelo plano temos:
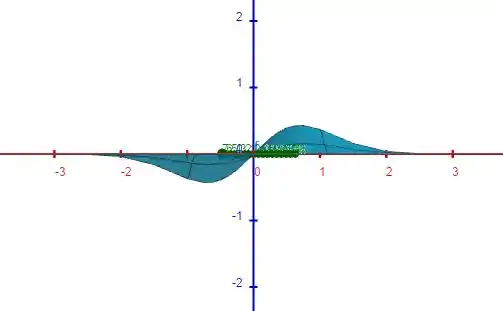
Agora uma vista geral:
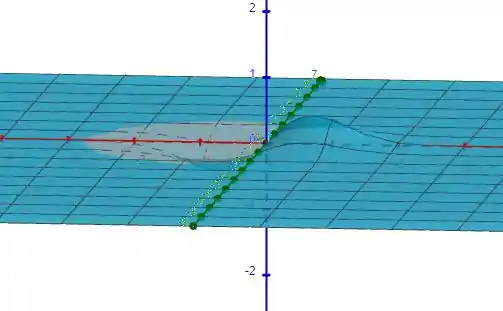
Gráfico de :
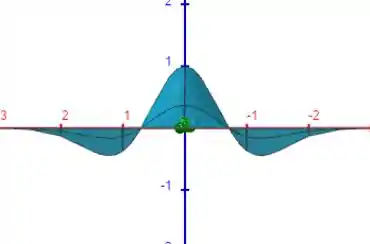
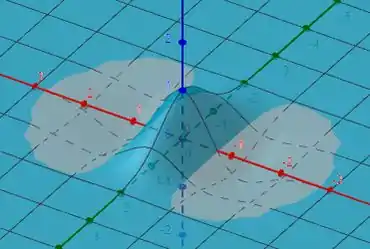
Observe como o gráfico de nos mostra exatamente o comportamento da função original: Nos pontos de máximo e mínimo da função quando apenas varia, o gráfico de mostra dois zeros.
Gráfico de :
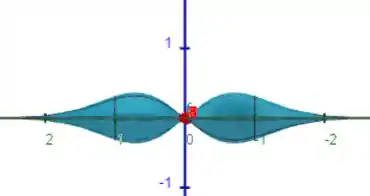
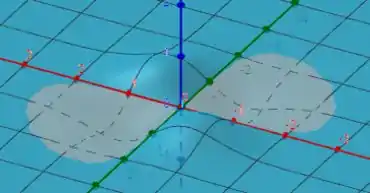
Da mesma forma o gráfico de nos apresenta muitos detalhes sobre a função original, observe por exemplo o comportamento das “barriguinhas” nos respectivos quadrantes, tendendo a crescer ou diminuir o valor de de modo a formar essas concavidades