Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 1.Exercícios de Revisão - Ex. 17
Determine um intervalo, no qual define uma solução para .
Passo 1
Olha só uma coisa que temos que reparar pra resolver esse problema: a expressão nunca é menor que , e podemos comprovar isso verificando que seu comportamento de acordo com os valores de é uma parábola com vértice
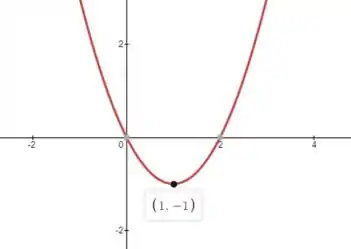
Então:
Mas também temos que deve ser uma solução, então:
Então, resolvendo a inequação, temos que o intervalo procurado é
Resposta
Exercícios de Livros Relacionados
Por inspeção, determine, se possível, uma solução real para a equação diferencial dada. d y d x + y = 0 d y d x + y + 1 = 0 d y d x + y = 1
Nos problemas 49 e 50, encontre valores de m para que y = x m seja uma solução para cada equação diferencial. x 2 y ' ' - 6 x y ' + 4 y = 0
Nos problemas 47 e 48, encontre valores de m para que y = e m x seja uma solução para cada equação diferencial. y ' ' - 5 y ' + 6 y = 0
Mostre que y 1 = 2 x + 2ey 2 = - x 2 2 são ambas soluções para y = x y ' + y ' 2 2 As funções c 1 y 1ec 2 y 2 , com c 1 ec 2 constantes arbitrárias são também soluções? A soma y 1 + y 2 é uma solução?
Mostre que y 1 = x 2ey 2 = x 3 são ambas soluções para x 2 y ' ' - 4 x y ' + 6 y = 0 As funções c 1 y 1ec 2 y 2 , com c 1 ec 2 constantes arbitrárias são também soluções? A soma y 1 + y 2 é uma soluçã