Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.3 - Ex. 43
- Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescente
- Identifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem
Passo 1
Primeiramente, necessitamos calcular a derivada de para encontrar os pontos críticos
Igualamos a zero
Galera, aqui podemos utilizar a seguinte propriedade de logaritmos . Sabendo disso, como , façamos:
Pontos críticos:
Passo 2
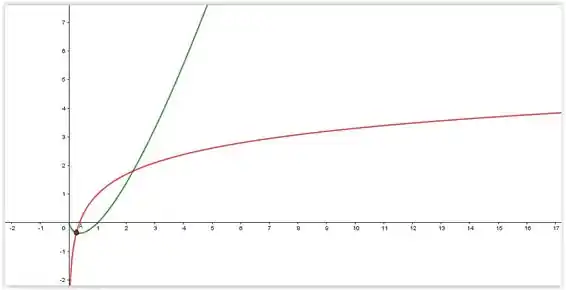
Observando o gráfico da função, temos que , representado pelo ponto A, é ponto de mínimo local e absoluto da função. Não há máximos locais, nem absoluto.
Resposta
- Função é sempre crescente
- B) O ponto A é o mínimo local e não há máximos locais nem absolutos.
Exercícios de Livros Relacionados
Considere duas retas paralelas r e s. Sejam A e C dois pontos distintos de r e B um ponto de sDetermine Q na reta s de modo que a soma das áreas dos triângulos APC e QPB seja mínima
Dado o triângulo retângulo de catetos 3 e 4, determine o retângulo de maior área nele inscrito, de modo que um dos lados esteja contido na hipotenusa.
Seja x 0 , y 0 , x 00 e y 00 , um ponto da elipse x 2 + 4 y ² = 1 ² . Seja T a reta tangente à elipse no ponto ( x 0 , y 0 ) .Verifique que T tem por equação x 0 x + 4 y 0 y = 1 Determine x 0 de modo
Dois vértices de um retângulo R estão sobre o eixo x e os outros dois sobre o gráfico de y = x 1 + x 2 , x0 . Considere o cilindro que se obtém girando o retângulo R em torno do eixo x . Determine o r
(Teorema de Darboux.) Suponha g derivável em [ a , b ] . Com g ' a0 e g ' b0 . Prove que existe c em ] a , b [ tal que g ’ ( c ) = 0