Dado o triângulo retângulo de catetos 3 e 4, determine o retângulo de maior área nele inscrito, de modo que um dos lados esteja contido na hipotenusa.

Oi, galerinha! Tudo bom? Para resolver essa questão vamos primeiro desenhar o nosso triângulo retângulo, com um retângulo dentro dele. É importante notar que a hipotenusa é 5. A figura fica assim então:

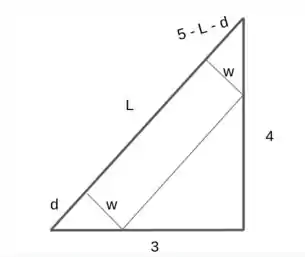
Agora que entendemos a nossa figura vamos achar uma equação para a área do retângulo.

Podemos tirar das relações de proporcionalidade de triângulos retângulos que (para o triangulo inferior formado pelos catetos e ):

(Para o triangulo superior):

Portanto:

Agora temos os tamanhos da base e do lado do retângulo, assim a área é:

Agora vamos maximizar essa função!