Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 9.6 - Ex. 26
Seja , e , um ponto da elipse . Seja a reta tangente à elipse no ponto .
- Verifique que tem por equação
- Determine de modo que a área do triângulo determinado por T e pelos eixos coordenados seja mínima.
Passo 1
Bem, primeiramente vamos reescrever a equação da elipse:
Dessa forma, podemos desenhar a elipse:
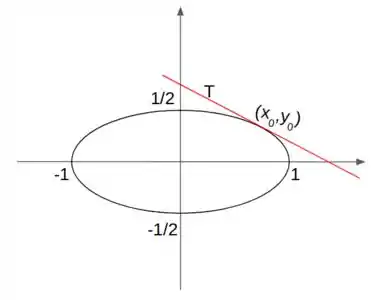
Passo 2
a) Bem, para determinar a reta tangente a um ponto, vamos utilizar a ideia de que o valor da derivada no ponto é o coeficiênte da reta. Para isso, vamos encontrar como função de :
Pelo enunciado, os pontos estão no primeiro quadrante, assim:
Derivando:
Dessa forma,
Agora, podemos aplicar a equação da reta tangente:
Utilizando a equação da elipse, temos que:
Portanto:
Passo 3
(b) Bem, vamos achar os pontos do triângulo formado pela reta e os eixos. Um ponto é quando e o outro quando , quando :
Agora, quando :
Assim, a área é dada por:
Porém, precisamos achar uma expressão para área em relação a , portanto vamos usar a seguinte relação:
Portanto,
Para achar o mínimo, vamos derivar e igualar a zero: