Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 3.16 - Ex. 3b
Analisar graficamente a existência de assíntotas para as seguintes funções:
Passo 1
O gráfico dessa função fica com essa cara aqui:
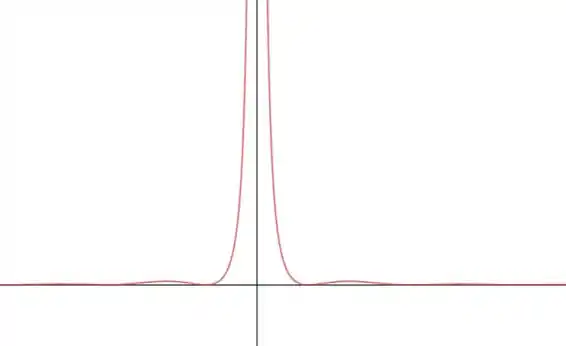
Passo 2
Analisando o gráfico, já vemos de cara que é uma assíntota horizontal. A reta tá com cara de assíntota vertical, então pra confirmar vamos tirar o zoom da figura.
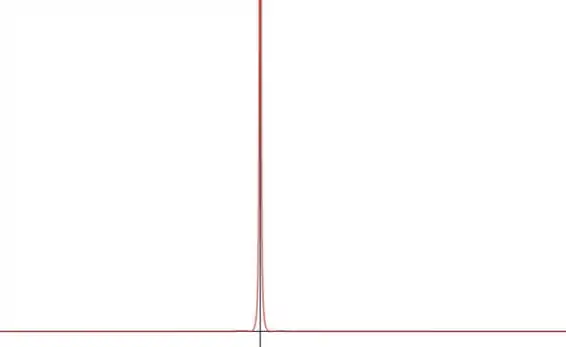
Vendo assim mais de longe não resta mais dúvida de que essa reta também é assíntota!
Resposta
é uma assíntota horizontal e é uma assíntota vertical.
Exercícios de Livros Relacionados
Encontre o limite ou demonstre que não existe. l i m y → ∞2-3 y 2 5 y 2+4 y
29. Encontre o limite ou demonstre que não existe. lim x → ∞ x 4 - 3 x 2 + x x 3 - x + 2
5. Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dada lim x → 0 f x = - ∞ lim x → - ∞ f x = 5lim x → ∞ f x = - 5
8. Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dada lim x → ∞ f x = 3 ,lim x → 2 - f x = ∞ ,lim x → 2 + f x = - ∞ , f é ímpar
7. Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dada lim x → 2 f x = - ∞lim x → ∞ f x = ∞lim x → - ∞ f x = 0 lim x → 0 + f x = ∞ lim x → 0 - f x = - ∞