Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 35
35. Determine o limite infinito.
Passo 1
Falaí pessoalzinho!
Gente, esse enunciado é meio estranho! Ele já nos diz que o limite é infinito, então não é isso que queremos focar em discutir.
O nosso objetivo aqui é entender o sinal desse resultado, se vai ser infinito positivo ou negativo.
E pra isso, precisamos reparar nesse sinalzinho de + que aparece na nossa expressão
Isso é uma nomenclatura de limites laterais. Significa que estamos considerando que tende a 5 somente por um lado. No caso, como o sinal é de positivo, estamos nos aproximando de pela direita, ou seja, por valores maiores que 5.
Então vamos calcular considerando isso!
Passo 2
Primeiro vamos associar o argumento do a uma única variável:
Então quando ,
Podemos escrever então que:
Agora se analisarmos o comportamento de para valores muito pequenos, proximos de zero, vemos que a função também decresce pra valores muiiito pequenos:
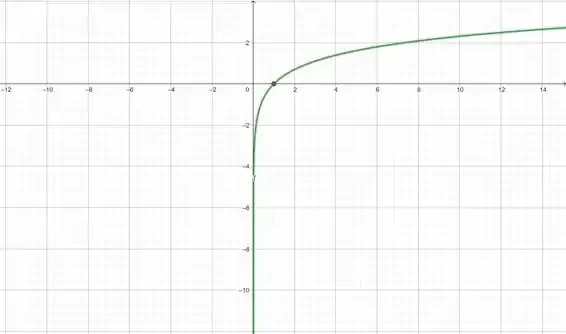
Ou seja, o limite será infinito, porém para valores negativos: